Tìm a, b để đa thức \(A\left( x \right) = 2{x^3} – {x^2} + ax + b\) chia hết cho đa thức \(B(x) = {x^2} – 1.\) … trong Đề kiểm tra 15 phút Đề số 4 Bài 12 Chương 1 Đại số 8. Xem Đề và đáp án đầy đủ phía dưới đây

Bài 1. Tìm a, b để đa thức \(A\left( x \right) = 2{x^3} – {x^2} + ax + b\) chia hết cho đa thức \(B(x) = {x^2} – 1.\)
Bài 2. Tìm x để phép chia \(\left( {5{x^3} – 3{x^2} + 7} \right):\left( {{x^2} + 1} \right)\) có dư bằng 5.

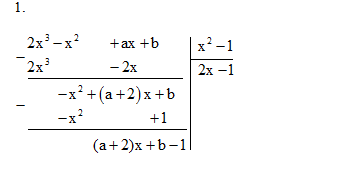
Advertisements (Quảng cáo)
A(x) chi hết cho B(x) khi \(\left( {a + 2} \right)x + b – 1\) là đa thức 0.
Vậy \(a + 2 = 0\) và \(b – 1 = 0 \Rightarrow a = – 2\) và \(b = 1.\)
2.
Advertisements (Quảng cáo)
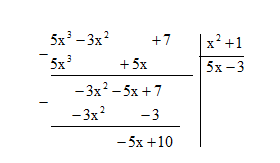
Ta có \( – 5x + 10 = 5 \Rightarrow – 5x = – 5 \Rightarrow x = 1.\)






