
I. PHẦN TRẮC NGHIỆM: (3 điểm )
1. : Cho a> b và a.b<0, bất đẳng thức \(\dfrac{1}{a} > \dfrac{1}{b}\) là đúng hay sai ?
A. Đúng B.Sai
2. : Hai phương trình cùng nhận x= a làm nghiệm có tương đương với nhau không?
A. Có B. không
3.: Giải phương trình \(2{x^2} – 2x + 1 = – 5x\)
A. x= -1
B. x= \(\dfrac{1}{2}\)
C. x= 1
D.x = -1; x= -\(\dfrac{1}{2}\)
4. : Viết tập nghiệm của bất phương trình bằng kí hiệu tập hợp:
\( – 7 \ge 5x\)
A. \(S = \left\{ {x \in R/x \le – \dfrac{7}{5}} \right\}\)
B. \(S = \left\{ {x \in R/x \ge \dfrac{7}{5}} \right\}\)
C. \(S = \left\{ {x \in R/x \le \dfrac{7}{5}} \right\}\)
D.\(S = \left\{ {x \in R/x \ge – \dfrac{7}{5}} \right\}\)
5. : Cho hình hộp chữ nhật có ba kích thước 5cm,3cm,2cm. Tính thể tích của hình hộp đó
A. 30cm
B. 30 cm2
C. 10cm 3
D. 30cm3
6. : Tính tỉ số của các cặp đoạn thẳng sau :
AB=18cm,CD =12cm
A.\(\dfrac{5}{3}\)
B. \(\dfrac{3}{2}\)
C.\(\dfrac{1}{6}\)
D.\(\dfrac{{12}}{{15}}\)
Advertisements (Quảng cáo)
II. PHẦN TỰ LUẬN (7đ):
Bài 1: (2đ) Cho biểu thức : M = \(\left( {\dfrac{1}{{x + 1}} + \dfrac{2}{{1 – x}} + \dfrac{x}{{{x^2} – 1}}} \right):\dfrac{1}{{x + 1}}\)
a, Rút gọn biểu thức M.
b, Tính giá trị của biểu thức M khi x = -1 ; x = 2
Bài 2: (2đ)
a, Giải bất phương trình và biểu diễn tập nghiệm trên trục số : 3x – 12 ≥ 0
b, Cho ba số dương a, b, c có tổng bằng 1. Chứng minh : \(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge 9\)
Bài 3: (1đ)
Một xe ô tô đi từ A đến B với vận tốc 50 km/h . Lúc từ B trở về A xe đi với vận tốc 45km/h nên thời gian về nhiều hơn thời gian đi là 20 phút. Tính quãng đường AB.
Bài 4: (2đ)
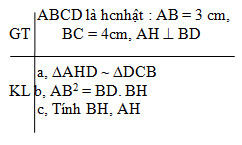
Cho hình chữ nhật ABCD , có AB = 3 cm , BC = 4 cm . Vẽ đường cao AH của tam giác ABD .
a, Chứng minh: ∆AHD ~ ∆DCB.
b, Chứng minh: AB2 = BH.BD .
c, Tính độ dài: BH, AH .
I/PHẦN TRẮC NGHIỆM:
1A; 2B; 3D; 4A; 5D; 6B
II/PHẦN TỰ LUẬN (7đ)
Bài 1: (2đ)
Advertisements (Quảng cáo)
a, Rút gọn biểu thức: Điều kiện xác định của biểu thức M là : x ≠ ±1
\(M=\left( {\dfrac{1}{{x + 1}} – \dfrac{2}{{x – 1}} + \dfrac{x}{{{x^2} – 1}}} \right)\)\(\,:\dfrac{1}{{x + 1}}\)
= \(\dfrac{{x – 1 – 2(x + 1) + x}}{{{x^2} – 1}}:\dfrac{1}{{x + 1}}\)
= \(\dfrac{{x – 1 – 2x – 2 + x}}{{{x^2} – 1}}:\dfrac{1}{{x + 1}}\)
=\(\dfrac{{ – 3}}{{(x – 1)(x + 1)}}.\dfrac{{x + 1}}{1}\) = \(\dfrac{{ – 3}}{{x – 1}}\)
= \(\dfrac{3}{{1 – x}}\)
b, Khi x = -1(không TMĐKXĐ) . Nên giá trị của biểu thức M không xác định.
Khi x = 2 ( TMĐKXĐ ).
M =\(\dfrac{3}{{1 – 2}}\) = \(\dfrac{3}{{ – 1}}\) = -3
Bài 2: (2đ)
a, 3x – 12 ≥ 0 \( \Leftrightarrow \) 3x ≥ 12 \( \Leftrightarrow \) x ≥ 4 . Vậy x ≥ 4 là nghiệm của bất phương trình đã cho.
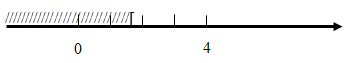
b, Ta có a + b + c = 1.
Nên \(\dfrac{{a + b + c}}{a}\)=\(\dfrac{1}{a} \)\(\;\Rightarrow \dfrac{1}{a}=1+\dfrac{b}{a} + \dfrac{c}{a}\,\,\,\,\,\,\,(1)\)
\(\dfrac{{a + b + c}}{b} = \dfrac{1}{b}\)\(\; \Rightarrow \dfrac{1}{b} = 1 + \dfrac{a}{b} + \dfrac{c}{b}\,\,\,\,\,\,\,(2)\)
\(\dfrac{{a + b + c}}{c} = \dfrac{1}{c}\)\(\; \Rightarrow \dfrac{1}{c} = 1 + \dfrac{a}{c} + \dfrac{b}{c}\,\,\,\,\,\,\,(3)\)
Vế cộng vế của (1),(2),(3) ta có:
\(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \)\(\,= 3 + \left( {\dfrac{a}{b} + \dfrac{b}{a}} \right) + \left( {\dfrac{b}{c} + \dfrac{c}{b}} \right)\)\(\, + \left( {\dfrac{c}{a} + \dfrac{a}{c}} \right)\)
Mà: a2 + b2 ≥ 2ab (Bất đẳng thức Cô-Si) \( \Rightarrow \dfrac{{{a^2} + {b^2}}}{{ab}} \ge \dfrac{{2ab}}{{ab}}\) \( \Rightarrow \dfrac{a}{b} + \dfrac{b}{a} \ge 2\)
Tương tự ta có: \(\dfrac{b}{c} + \dfrac{c}{b} \ge 2\) và : \(\dfrac{a}{c} + \dfrac{c}{a} \ge 2\)
Nên : \(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge 3 + 2 + 2 + 2 = 9\)
Vậy : \(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge 9\)
Bài 3:(1điểm)
Gọi quãng đường AB là x (km), điều kiện : x > 0 .
Thời gian ô tô đi từ A đến B với vận tốc 50 km/h là :\(\dfrac{x}{{50}}\) (h)
Thời gian ô tô đi từ B trở về A với vận tốc 45km/h là : \(\dfrac{x}{{45}}\) (h)
Mà thời gian về nhiều hơn thời gian đi là: 20 phút = \(\dfrac{1}{3}\)h, nên ta có phương trình:
\(\dfrac{x}{{45}} – \dfrac{x}{{50}} = \dfrac{1}{3}\) \( \Leftrightarrow \) 10x – 9x = 150
\( \Leftrightarrow \) x = 150 (TMĐK)
Vậy quãng đường AB là 150 km.
Bài 4: (2điểm)
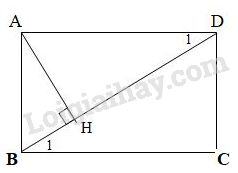
Chứng minh
a, Xét ∆AHD và ∆DCB có: H = C = 900(gt), D = B (so le trong do AD// CB) \( \Rightarrow\) ∆AHD~∆DCB(g.g)
b, Xét ∆ADB và ∆HAB có : Â = H = 900 (gt), B chung \( \Rightarrow\)∆ADB ~ ∆HAB (g.g)
\( \Rightarrow\) \(\dfrac{{AB}}{{HB}} = \dfrac{{BD}}{{AB}} \Rightarrow \) AB2 = BD.HB
c, ∆ADB vuông tại A, nên: DB2 = AB2 + AD2(đ/l Pi ta go)\( \Rightarrow\) DB2 = 32 + 42 = 25 = 52
\( \Rightarrow\)DB= 5(cm)
Vì AB2 = BD.HB (c/m trên)
\( \Rightarrow\) HB = \(\dfrac{{A{B^2}}}{{BD}} = \dfrac{{{3^2}}}{5} = \dfrac{9}{5} = 1,8(cm)\)
Vì ∆ADB ~∆HAB (c/m trên) \( \Rightarrow\) \(\dfrac{{AD}}{{AH}} = \dfrac{{BD}}{{AB}}\)
\(\Rightarrow AH = \dfrac{{AD.AB}}{{BD}} = \dfrac{{4.3}}{5} = 2,4(cm)\)
Vậy : BH = 1,8 cm ; AH = 2,4 cm



![[THCS Cự Khê] thi cuối năm môn Toán lớp 8: Cho ΔABC có AB = 8cm, AC = 12cm. Trên cạnh AB lấy điểm D sao cho BD = 2cm, trên cạnh AC lấy điểm E sao cho AE = 9cm. hứng minh: ΔADE đồng dạng ΔABC](https://dethikiemtra.com/wp-content/uploads/2020/09/images-100x75.jpg)


