Bài ôn tập chương 3 hình học 8: Bài 56,57,58, 59,60,61 trang 92 Toán lớp 8 tập 2

Đáp án và hướng dẫn Giải bài ôn tập chương 3 hình học 8: Bài 56,57,58, 59,60,61 trang 92 SGK Toán 8 tập 2 – Tam giác đồng dạng.

Chương 3: Tam giác đồng dạng (gồm có 9 bài)

1. Định lí Ta – lét trong Δ
2. Định lí đảo và hệ quả của định lí Talet
3. Tính chất đường phân giác của Δ
4. Khái niệm hai Δ đồng dạng
5. Trường hợp đồng dạng thứ nhất
6. Trường hợp đồng dạng thứ hai
7. Trường hợp đồng dạng thứ ba
8. Các trường hợp đồng dạng của Δ vuông
9. Ứng dụng thực tế của Δ đồng dạng
10. Giải bài ôn tập chương 3 hình học 8

Bài 56. Xác định tì số của hai đoạn thẳng AB và CD trong các trường hợp sau :

a) AB = 5cm, CD = 15cm ;

b) AB = 45dm,  CD = 150cm ;

c) AB = 5

Giải: a) AB/CD = 5/15 = 1/3

b) Ta có: AB = 45dm = 450cm và CD =150cm =15 dm
AB/CD = 45/15 = 3 hoặc AB/CD = 450/150 = 3

c) Ta có: AB = 5CD ⇒ AB/CD = 5CD/CD = 5 với chọn đoạn thẳng CD = 1 (đơn vị đo)

---

Bài 57 trang 92. Cho ΔABC (AB < AC). vẽ đường cao AH, đường phân giác AD, đường trung tuyến A. Có nhận xét về vị trí của ba điểm H,D,M.

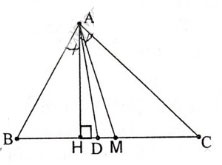
Ta có AD là phân giác góc BAC của ΔABC
⇒ DB/DC = AB/AC mà AB<AC
⇒ DB/DC < 1 ⇒ DB <DC
AM là trung tuyến của ΔABC ⇒ BM = MC
DB < DC ⇒ DB + DC < DC + CD ⇒ BC < 2DC
⇒ 2MC < 2DC ⇒ MC < DC ⇒ M nằm giữa hai điểm D và C (1)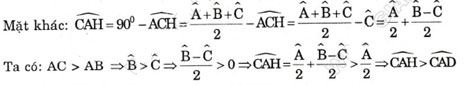

⇒ Tia AD nằm giữa hai tia AC và AH (2)
Từ (1) và (2) ta có: điềm D nẵm giữa hai điểm H và M.

---

Bài 58 . Cho Δcân ABC (AB = AC), Vẽ các đường cao BH, CK (h.66).

a) Chứng minh BK = CH.

b) Chứng minh KH//BC.

c) Cho biết BC = a, AB = AC = b. Tính dộ dài đoạn thầne HK.

Hướng dẫn câu c)

• Vẽ thêm đường cao AI, xét hai Δ đồng dạng IAC và HBC rồi tính CH
• Tiếp theo, xét hai Δ đồng dạng AKH và ABC rồi tính HK.

Giải: a) Xét hai Δvuông HBC và ΔKCB

∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung

⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)

⇒ CH = BK

b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK

AK = AB – BK và AH = AC – CH ⇒ AK = AH

⇒ AK/AB = AH/AC ⇒ KH//BC

c) Kẻ đường cao AI của Δ ABC và xét Δ IAC

ΔHBC có ∠ACI = ∠BCH

⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a²/2b

---

Bài 59. Hình thang ABCD (AB // CD) có AC và BD cắt nhau lại O, AD và BC cắt nhau lại K. Chứng minh rằng OK đi qua trung điếm của các cạnh AB và CD.

Giải: 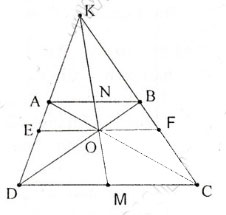Vẽ đường thẳng EF đi qua O và song song CD.
Ta có EO//DC ⇒ OE/DC = AO/AC (1)
OF//DC ⇒ OF/DC = BO/BD (2)
Ta có: AB//DC ⇒ OA/OC = OB/OD
⇒ OA/ (OC + OA) = OB/(OD+ OB) ⇒ OA/AC = OB/BD (3)
Từ (1),(2),(3) ta có OE/DC = OF/DC ⇒ OE = OF
Ta có AB//EF
⇒ AN/EO = KN/KO và BN/FO = KM/KO
⇒ AN/EO = BN/FO ⇒ AN = BN
Tương tự: FE//DC ⇒ EO/DM = KO/KM
và FO/CM = KO/KM ⇒EO/DM=FO/CM ⇒ DM=CM

suy ra đường thẳng OK đi qua trung điểm của các cạnh AB và CD.

---

Bài 60 trang 92 Toán hình 8 tập 2. Cho Δvuông ABC. ∠A = 90°, C = 30° và đường phân giác BD (D thuộc cạnh AC).

a) Tính tỉ số AD/CD

b) Cho biết độ dài AB = 12,5cm, hãy tính chu vi và diện tích của ΔABC.

Giải: a) Ta có ΔABC vuông tại A và ∠C = 300
⇒AB = 1/2BC ⇒ BC = 2AB
Vì BD là phân giác ⇒ DA/DC = AB/BC = AB/2AB =1/2
b) AB = 12,5 cm ⇒ BC = 25 cm

Áp dụng định lí pitago vào ΔABC vuông tại A ta có :f

AC²= BC² – AB² = 25² – 12,5²

AC = 21,65 (cm)

C_ABC = AB+ BC+ CA =12,5+25+21,65 = 59,15(cm)

S_ABC = 1/2AB.AC =1/2.12,5.21,65 = 135,31 (cm2)

---

Bài 61. Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm, DA = 8cm, đường chéo BD = 10cm.

a) Nêu cách vẽ tứ giác ABCD có kích thước đã cho ở trên

b) Các ΔABD và BDC có đồng dạng với nhau không ? Vì sao ?

c) Chứng minh rằng AB//CD

Đáp án: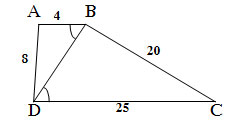

a)Vẽ ΔBDC có BD = 10c,, DC =25cm và BC = 20cm
– Vẽ DC = 25 cm
– Vẽ đường tròn tâm D, bán kính R = 10cm và đường tròn tâm C, bán kính R = 20cm và giao điểm của 2 đường tròn trên là điểm B
* Vẽ điểm A: vẽ đường tròn tâm B, bán kính bằng 4 cm và đường tròn tâm D, bán kính bằng 8 cm. Giao điểm của hai đường tròn là A.
Tứ giác ABCD thỏa mãn các điều kiện bài toán.

b) Ta có AB/BD = 4/10 =2/5; BD/DC =10/25=2/5 và AD/BC = 8/20 =2/5
⇒ AB/BD = BD/DC = AD/BC = 2/5 ⇒ ΔABD ∽ ΔBDC
c) Ta có ΔABD ∽ ΔBDC ⇒ góc ∠ABD = ∠BDC ⇒ AB//DC