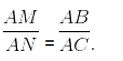Luyện tập 2 – Trường hợp đồng dạng thứ ba: bài 41, 42, 43, 44, 45 trang 80 SGK Toán 8 tập 2.
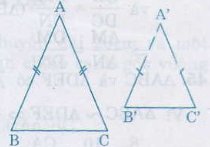
Bài 41. Tìm dấu hiệu nhận biết hai tam giác cân đồng-dạng.
Từ trường hợp 1 ta có:
– Nếu cạnh bên và cạnh đáy của Δcân này tỉ lệ với cạnh bên và cạnh đáy của Δcân kia thì hai Δ đó đồng-dạng.
Từ trường hợp 2 và 3 ta nói:
– Nếu hai Δcân có một góc tương ứng bằng nhau thì hai Δ đó đồng-dạng.
Bài 42. So sánh các trường hợp đồng-dạng của tamgiác với các trường hợp bằng nhau của tam giác (nêu lên những điểm giống nhau và nhau).
|
Trường hợp |
Giống nhau |
Khác nhau |
|
|
Bằng nhau |
Đồngdạng |
||
|
1 |
3 cạnh |
3 cạnh tương ứng = |
3 cạnh tương ứng tỉ lệ |
|
2 |
2 cạnh một góc |
Cạnh cạnh tương ứng và một góc kề với hai cạnh = |
2 cạnh tương ứng tỉ lệ |
|
3 |
1 cạnh và hai góckề tương ứng = |
2góc tương ứng = |
|
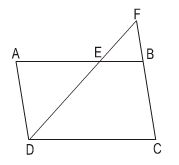
Bài 43 trang 80. Cho hình bình hành ABCD(h46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt CB kéo dài tại F,
a) Trong hình vẽ đã cho có bao nhiêu cặp Δ đồngdạng? hãy viết các cặp Δđồngdạng với nhau theo các đỉnh tương ứng.
b) Tính độ dài đoạn EF và BF, biết rằng DE = 10cm.
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
Advertisements (Quảng cáo)
b) BE = AB – AE = 12 – 8 = 4cm
∆ADE ∽ ∆BFE =>
=> BF = 3,5 cm.
EF = 5 cm.
Bài 44 Toán 8. Cho ΔABC có các cạnh AB= 24cm, AC = 28cm. Tia phân giác của ∠A cắt cạnh BC tại D. Gọi M,N theo thứ tự là hình chiếu của B và C trên AD.
a) Tính tỉ số BM/CN
Advertisements (Quảng cáo)
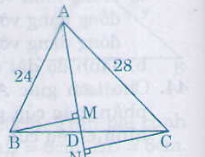
a) AD là đường phân giác của ∆ABC
Mà BM // CN (cùng ⊥ với AD).
=> ∆BMD ∽ ∆CND
b)
∆ABM và ∆ACN có:
∠ABM = ∠CAN = 900
=> ∆ABM ∽ ∆ACN =>
Bài 45 trang 80. Hai ΔABC và ΔDEF có ∠A = ∠B; ∠D = ∠E, AB = 8cm, BC = 10cm, DE= 8cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.
∆ABC ∽ ∆DEF vì có ∠A = ∠B; ∠D = ∠E nên đồng dạng.
Vì ∆ABC ∽ ∆DEF =>
Suy ra: EF = 7,5 cm
=> CD = 8.3 / 2 = 12 cm
FD = 12 -3 = 9cm