Bài 1: Cho tam giác ABC biết BC = 1cm; AB = 6cm. Tính độ dài cạnh AC biết độ dài này là một số nguyên.
Bài 2: Chứng minh rằng “trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy”.
Bài 3: Cho tam giác ABC có AB = 6cm; AC = 12cm; BC = 15cm.
a) Chứng minh rằng \(\Delta ABC\) vuông.
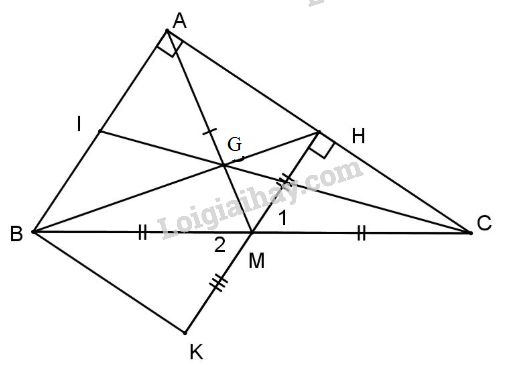
b) Vẽ trung tuyến AM. Từ M vẽ MH vuông góc với AC. Trên tia đối của tia MH lấy điểm K sao cho MK = MH. Chứng minh \(\Delta MHC = \Delta MKB.\)
c) Gọi G là giao điểm của BH và AM. Gọi I là trung điểm của AB. Chứng minh rằng I, G, C thẳng hàng.

Bài 1: Ta có \(6 – 1,AC < 6 + 1\) hay \(5 < AC < 7\) mà độ dài AC là một số nguyên nên AC = 6cm.
Bài 2:
Advertisements (Quảng cáo)
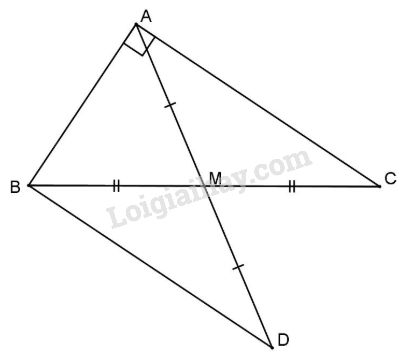
Trên tia đối của tia MA lấy D sao cho MD = MA khi đó ta có \(\Delta AMC = \Delta DMB\) (c.g.c)
\( \Rightarrow AC = B{\rm{D}}\) và \(\widehat C = {\widehat B_1}\)
\( \Rightarrow B{\rm{D}}\) // AC (có cặp góc so le trong bằng nhau)
Mà \(AC \bot AB\) (gt)
\( \Rightarrow B{\rm{D}} \bot AB\) hay \(\widehat {AB{\rm{D}}} = {90^0}\).
Advertisements (Quảng cáo)
Xét hai tam giác vuông ABD và BAC có AB chung, AC = BD (cmt).
Do đó \(\Delta AB{\rm{D}} = \Delta BAC\) (c.g.c)
\( \Rightarrow A{\rm{D}} = BC\) mà \(AM = \dfrac{1}{ 2}A{\rm{D}} \Rightarrow AM = \dfrac{1 }{2}BC.\)
Bài 3:
a) Ta có
\(B{C^2} = A{B^2} + A{C^2}{\rm{ }}({15^2} = {9^2} + {12^2}).\)
Theo định lý Pytago đảo \(\Delta ABC\) vuông tại A.
b) Xét \(\Delta MHC\) và \(\Delta MKB\) có
+) MC = MB (gt);
+) \({\widehat M_1} = {\widehat M_2}\) (đối đỉnh);
+) MH = MK (gt).
Do dó \(\Delta MHC = \Delta MKB\) (c.g.c)






