Bài 1: Cho tam giác ABC vuông tại A, đường cao AH, các đường phân giác của góc \(\widehat {BAH}\) và \(\widehat {CAH}\) cắt BC ở D và E.
a) Chứng minh \(\widehat {HAB} = \widehat {C.}\)
b) Chứng minh \(\Delta ABE\) cân.
Bài 2: Cho tam giác ABC có \(AB < AC\), phân giác AD. Trên tia AC lấy điểm E sao cho \(A{\rm{E}} = AB.\)
a) Chứng minh: \(B{\rm{D}} = E{\rm{D}}.\)
b) AB cắt ED ở K. Chứng minh rằng: \(\Delta DBK = \Delta DEC.\)
c) Chứng minh: \(\Delta AKC\) là tam giác đều.
d) Chứng minh: \(A{\rm{D}} \bot KC.\)

Bài 1:
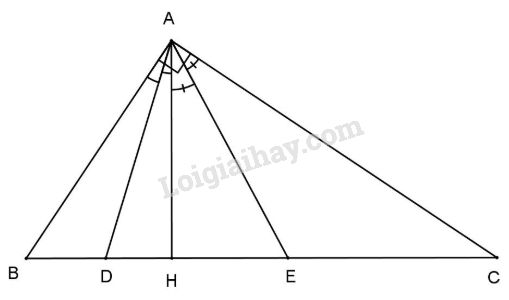
Advertisements (Quảng cáo)
a) Ta có \(\Delta ABC\) vuông tại A nên \(\widehat B + \widehat C = {90^0}\).
\(\Delta AHB\) vuông cân tại H nên
\(\widehat B + \widehat {BAC} = {90^0}\)
\( \Rightarrow \widehat {BAH} = \widehat C.\)
b) Mặt khác AE là tia phân giác của \(\widehat {A{\rm{E}}B} = \widehat C + \widehat {CA{\rm{E}}}\) (góc ngoài \(\Delta A{\rm{E}}C\))
\( \Rightarrow \widehat {BAH} + \widehat {HA{\rm{E}}} = \widehat {A{\rm{E}}B}\) hay \(\widehat {E{\rm{A}}B} = \widehat {A{\rm{E}}B}.\)
Chứng tỏ \(\Delta ABE\) cân tại B.
Bài 2:
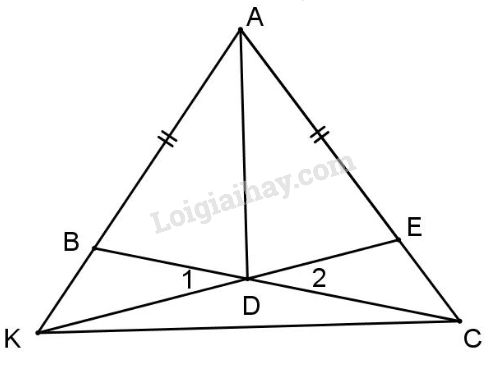
a) Xét \(\Delta A{\rm{D}}B\) và \(\Delta A{\rm{D}}E\) có:
Advertisements (Quảng cáo)
+) AD cạnh chung;
+) \({\widehat A_1} = {\widehat A_2}\) (gt);
+) \(AB = A{\rm{E}}\) (gt).
Do đó \(\Delta A{\rm{D}}B = \Delta A{\rm{D}}E\) (c.g.c)
b) \(\Delta A{\rm{D}}B = \Delta A{\rm{D}}E\)(cmt)
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {A{\rm{ED}}}\) (góc tương ứng),
mà \(\widehat {AB{\rm{D}}} + \widehat {A{\rm{ED}}} = {180^0}\) (kề bù).
Tương tự \(\widehat {A{\rm{ED}}} + \widehat {CE{\rm{D}}} = {180^0}\)
\( \Rightarrow \widehat {BK{\rm{D}}} = \widehat {CE{\rm{D}}}.\)
Xét \(\Delta KB{\rm{D}}\) và \(\Delta CE{\rm{D}}\) có:
+) \({\widehat D_1} = {\widehat D_2}\) (đối đỉnh);
+) DB = DE (cmt);
+) \(\widehat {K{\rm{D}}B} = \widehat {CE{\rm{D}}}\) (cmt).
Do đó \(\Delta DBK = \Delta DEC\) (g.c.g).
c) Ta có \(AB = A{\rm{E}}\) (gt), \(\Delta \Delta {\rm B}{\rm K} = \Delta DEC\) (cmt) \( \Rightarrow BK = EC\) (cmt) \( \Rightarrow AB + BK = A{\rm{E}} + EC\) hay \(AK = AC.\)
d) \(\Delta ABC\) cân tại A (cmt); có AD là phân giác (gt) nên AD cũng đồng thời là đường cao, hay \(A{\rm{D}} \bot KC.\)
Vậy \(\Delta AKC\) cân tại A.






