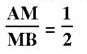Khái niệm hai tam giác đồng dạng: giải bài 23 trang 71; bài 24, 25, 26, 27, 28 trang 72 SGK Toán 8 tập 2.
Bài 23. Trong hai mệnh đề sau, mệnh đề nào đúng? Mệnh đề nào sai?
a) Hai Δ bằng nhau thì đồng dạng với nhau.
b) Hai Δ đồng-dạng với nhau thì bằng nhau
Đáp án: a) a là mệnh đề đúng.
b) b là mệnh đề sai
Bài 24 trang 72. ∆A’B’C’ ∽ ∆A”B”C” theo tỉ số đồng dạng K1, ∆A”B”C” ∽∆ ABC theo tỉ số đồng dạng k2. Hỏi ΔA’B’C’ đồng dạng với ΔABC theo tỉ số nào?
Giải: ∆A’B’C’ ∽ ∆A”B”C” theo tỉ số đồng dạng K1 = A’B’ / A”B”
∆A”B”C” ∽∆ ABC theo tỉ số đồng dạng k2 = A”B”/AB
Theo tính chất 3 thì ∆A’B’C’ ∽ ∆ABC.
vậy K= K1.k2
Bài 25. Cho ΔABC. Hãy vẽ một tam giác đồng dạng với ΔABC theo tỉ số 1/2.
Giải: Lấy trung điểm M của AB, N là trung điểm của AC => MN là đường trung bình của ΔABC.
=> MN // BC.
=> ∆ AMN ∽ ∆ABC theo tỉ số K = 1/2.
Advertisements (Quảng cáo)
Bài 26. Cho Δ ABC vẽ ΔA’B’C’ đồng dạng với ΔABC theo tỉ số đồng dạng là K = 2/3.
Trên cạnh AB lấy điểm M sao cho AM= 2/3 AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K= 2/3
Dựng ∆A’B’C’ = ∆AMN(theo trường hợp cạnh cạnh cạnh)
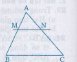
Bài 27 – Toán 8 tập 2. Từ M thuộc cạnh AB của ΔABC với AM= 1/2 MB. Kẻ các tia song song với AC, BC. Chúng cắt BC và AC lần lượt tại L và N.
a) Nêu tất cả các cặp tam giác đồng-dạng.
Advertisements (Quảng cáo)
b) Đối với mỗi cặp Δ đồng-dạng, hãy viết các cặp góc bằng nhau và tỉ số đồng dạng tương ứng.
a) MN // BC => ∆AMN ∽ ∆ABC
ML // AC => ∆MBL ∽ ∆ABC
và ∆AMN ∽ ∆MLB
Từ kết quả câu a ta có:
ΔAMN ∽ ΔABC
⇒ góc M1 = góc B; ∠N1 = ∠C; ∠A chung
Tỉ số đồng dạng:
ΔMBL ∽ ΔABC ⇒ góc ∠M2 = ∠A; ∠L1 = ∠C; ∠B chung
Tỉ số đồng dạng:
ΔAMN ∽ ΔMBL ⇒ ∠A = ∠M2; ∠M1 = ∠B; ∠N1 = ∠L1
Tỉ số đồng dạng:
Bài 28.∆A’B’C’ ∽ ∆ABC theo tỉ số đồng dạng K= 3/5.
a) Tính tỉ số chu vi của hai Δ đã cho.
b) Cho biết chu vi của hai Δ trên là 40dm, tính chu vi của mỗi tam giác.
Giải: a) ∆A’B’C’ ∽ ∆ABC theo tỉ số đồng dạng K= 3/5
Áp dụng tính chất của dãy tỉ số bằng nhau.
vậy tỉ số chu vi của ∆A’B’C’ và ∆ABC là 3/5.
=> CABC = 100 dm
CA’B’C’ = 60 dm