Hàm số nào sau đây có tập xác định R?; Cho tam giác ABC vuông tại A; \(AB = a;\,\,BC = 2a\). Tích vô hướng \(\overrightarrow {AC} .\overrightarrow {CB} \) bằng bao nhiêu? … trong Đề thi học kì 1 lớp 10 môn Toán. Xem Đề và đáp án đầy đủ phía dưới đây

A. TRẮC NGHIỆM (6đ)
1. : Xét tính chẵn, lẻ của hai hàm số \(f\left( x \right) = \left| {x + 10} \right| + \left| {x – 10} \right|;\)\(\,\,g\left( x \right) = – {\left| x \right|^2}\)
A. f(x) là hàm số chẵn, g(x) là hàm số lẻ.
B.f(x) là hàm số chẵn, g(x) là hàm số chẵn.
C. f(x) là hàm số lẻ, g(x) là hàm số chẵn.
D. f(x) là hàm số lẻ, g(x) là hàm số lẻ.
2. : Mệnh đề nào sau đây đúng?
A. \(\exists x \in Q;\,\,4{x^2} – 1 = 0\)
B. \(\exists x \in N;\,\,{n^2} + 1\) chia hết cho 4.
C. \(\forall x \in N;\,\,{n^2} > n\).
D. \(\forall x \in R;\,\,{\left( {x – 1} \right)^2} \ne x – 1\)
3. : Cho tam giác ABC với \(A\left( {4;3} \right);\,\,B\left( { – 5;6} \right);\,\,C\left( { – 4; – 1} \right)\). Toạ độ trực tâm H của tam giác ABC là:
A. \(\left( { – 3;2} \right)\) B. \(\left( { – 3; – 2} \right)\)
C. \(\left( {3; – 2} \right)\) D. \(\left( {3;2} \right)\)
4. : Cho tam giác ABC vuông tại A; \(AB = a;\,\,BC = 2a\). Tích vô hướng \(\overrightarrow {AC} .\overrightarrow {CB} \) bằng
A. \({a^2}\) B. \( – 3{a^2}\)
C. \( – {a^2}\) D. \(3{a^2}\)
5. : Hàm số nào sau đây có tập xác định R?
A. \(y = \dfrac{{2{x^2} – 5x}}{{{x^2} + x + 1}}\)
B. \(y = \dfrac{{2{x^2} – 5x}}{{x + 1}}\)
C. \(y = \dfrac{{2{x^2} – 5x}}{{{x^3} + 1}}\)
D. \(y = \dfrac{{2{x^2} – 5x}}{{{x^2} – 1}}\)
6. : Phát biểu nào sau đây là mệnh đề đúng.
A. Số 141 chia hết cho 3 \(\overrightarrow {AB} \) 141 chia hết cho 9.
B. 81 là số chính phương \(\overrightarrow {AD} \) \(\overrightarrow {AO} \) là số nguyên.
C. 7 là số lẻ \(\overrightarrow {AC} \) 7 chia hết cho 2
D. 3.5 = 15 \(\overrightarrow {DB} \) Bắc Kinh là thủ đô của Hàn Quốc.
7. : Trong mặt phẳng với hệ toạ độ Oxy, các vectơ đơn vị là \(\overrightarrow i \) và \(\overrightarrow j \). Tập hợp các điểm M sao cho \(\overrightarrow {OM} = \left( {2\cos t + 3} \right)\overrightarrow i + \left( {2 – \cos t} \right)\overrightarrow j \) là:
A. Đoạn thẳng IJ của đường thẳng \(y = – \dfrac{1}{2}x + \dfrac{7}{2}\) với \(I\left( {1;3} \right);\,\,J\left( {5;1} \right)\).
B. Đường thẳng \(y = – \dfrac{1}{2}x + \dfrac{7}{2}\).
C. Phần đường thẳng \(y = – \dfrac{1}{2}x + \dfrac{7}{2}\) trừ điểm \(J\left( {5;1} \right)\).
D. Phần đường thẳng \(y = – \dfrac{1}{2}x + \dfrac{7}{2}\) trừ điểm \(I\left( {1;3} \right)\).
8. : Cho hai số thực a và b thỏa mãn \(a < b\), cách viết nào sau đây là đúng.
A. \(\left\{ a \right\} \in \left[ {a;b} \right]\).
B. \(a \in \left( {a;b} \right]\).
C. \(a \subset \left[ {a;b} \right]\).
D. \(\left\{ a \right\} \subset \left[ {a;b} \right]\)
9. : Cho hàm số \(y = f\left( x \right) = \dfrac{x}{2} + \dfrac{2}{{x – 1}}\) với \(x > 1\). Giá trị nào của x thì hàm số đạt giá trị nhỏ nhất
A. 4. B. 2.
C. 3. D. \(\overrightarrow {MA} \).
1.0 : Cho \(a + b = 1\). Giá trị lớn nhất của \(B = a{b^2}\) bằng
A. \(\dfrac{4}{{27}}\) khi \(a = \dfrac{2}{3};\,\,b = \dfrac{1}{3}\).
B. \(\dfrac{2}{{27}}\) khi \(a = \dfrac{1}{3};\,\,b = \dfrac{2}{3}\)
C. \(\dfrac{4}{{27}}\) khi \(a = \dfrac{1}{3};\,\,b = \dfrac{2}{3}\)
D. \(\dfrac{4}{{27}}\) khi \(a = \dfrac{1}{2};\,\,b = \dfrac{1}{2}\)
1.1 : Cho \(A = \left\{ {2;5} \right\};\,\,B = \left\{ {2;3;5} \right\}\). Tập hợp \(A \cup B\) bằng tập hợp nào sau đây?
A. \(\left\{ {2;3;5} \right\}\) B.\(\left\{ {2;5} \right\}\)
C. \(\left\{ {2;3} \right\}\) D. \(\left\{ 5 \right\}\)
Advertisements (Quảng cáo)
1.2 : Giá trị nào của m thì phương trình \(m{x^2} + 2\left( {m + 3} \right)x + m = 0\) có hai nghiệm phân biệt cùng dấu?
A. \(m < – \dfrac{3}{2}\)
B. \(m > – \dfrac{3}{2}\) và \(m \ne 0\).
C. \( – \dfrac{3}{2} < m < 0\).
D. \(m \ne 0\)
1.3 : Cho phương trình \(\left( {{x^2} + 9} \right)\left( {x – 9} \right)\left( {x + 9} \right) = 0\). Phương trình nào sau đây tương đương với phương phương trình đã cho?
A. \(x + 9 = 0\)
B. \(x – 9 = 0\)
C. \(\left( {x – 9} \right)\left( {x + 9} \right) = 0\)
D. \({x^2} + 9 = 0\)
1.4 : Trong các bất đẳng thức sau, bất đẳng thức nào sai?
A. \(a > 0;\,\,b > 0\), ta có \(a + b \le \sqrt {2\left( {{a^2} + {b^2}} \right)} \) .
B. \(a > b > 0;\,\,\dfrac{1}{b} > \dfrac{1}{a}\).
C. \({a^2} + {b^2} + ab < 0\,\,\forall a;b \in R\)
D. \({a^2} + {b^2} + {c^2} \ge ab + bc + ca\,\,\forall a;b;c \in R\).
1.5 : Cho hình vuông ABCD có tâm O. Trong các mệnh đề sau, tìm mệnh đề sai
A. \(\overrightarrow {AD} + \overrightarrow {DO} = – \dfrac{1}{2}\overrightarrow {CA} \)
B. \(\overrightarrow {AC} + \overrightarrow {DB} = 4\overrightarrow {AB} \)
C. \(\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AO} \)
D. \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CB} \)
1.6 : Cho các tập hợp sau: \(M = \left\{ {1;2;3} \right\};\,\,N = \left\{ {x \in N|x < 4} \right\};\)\(\,\,P = \left( {0; + \infty } \right);\)\(\,\,Q = \left\{ {x \in R|2{x^2} – 7x + 3 = 0} \right\}\) . Chọn kết quả đúng nhất
A. \(M \subset N;\,\,M \subset P;\,Q \subset P\)
B. \(N \subset P;\,\,Q \subset P\)
C. \(M \subset N\)
D. \(M \subset N;\,\,M \subset P\).
1.7 : Trong các hàm số sau, hàm số nào tăng trên khoảng \(\left( { – 1;0} \right)\).
A. \(y = x\)
B. \(y = \left| x \right|\)
C. \(y = {x^2}\)
D. \(y = \dfrac{1}{x}\).
1.8 : Số nghiệm của phương trình \({x^2} + 3x + 1 = \left( {x + 3} \right)\sqrt {{x^2} + 1} \) là
A. 3. B. 1.
C. 4. D. 2.
Advertisements (Quảng cáo)
1.9 : Cho tam giác ABC cân đỉnh A, \(\widehat B = {30^0};\,\,BC = 6\), M là điểm thuộc BC sao cho \(MC = 2MB\). Tính \(\overrightarrow {MA} .\overrightarrow {MC} \).
A. 4. B. 20.
C. 2\(\overrightarrow {NP} \). D. 4\(\overrightarrow {QR} \).
2.0 : Cho tam giác ABC. Nếu điểm D thỏa mãn hệ thức: \(\overrightarrow {MA} + 2\overrightarrow {MB} – 3\overrightarrow {MC} = \overrightarrow {CD} \) với M tùy ý thì D là đỉnh của hình bình hành:
A. ABED với E là trung điểm của BC.
B. ABCD.
C. ACED với B là trung điểm của EC.
D. ACBD.
2.1 : Cho \(y = \dfrac{{\sqrt {3x – 2a} }}{{x – a + 2}}\). Giá trị nào của a để y xác định với mọi \(x > – 1\).
A.\(a \le 1\)
B. \(a \le – \dfrac{3}{2}\).
C.\(a < 1\)
D.\(a < – \dfrac{3}{2}\)
2.2 : Cho tam giác ABC có \(A\left( {1; – 1} \right);\,\,B\left( {5; – 3} \right)\) và \(C \in Oy\), trọng tâm \(G \in Ox\). Tọa độ điểm C là:
A. \(\left( {0;2} \right)\) B. \(\left( {2;0} \right)\)
C. \(\left( {0; – 4} \right)\) D. \(\left( {0;4} \right)\)
2.3 : Giá trị nào của m thì phương trình \(m{x^2} – 2\left( {m – 2} \right)x + m – 3 = 0\) có hai nghiệm trái dấu?
A. \(m \ge 3\).
B. \(m < 3\)
C. \(0 < m < 3\)
D. \(m < 0\)
2.4 : Cho các vec-tơ \(\overrightarrow {OA} = \left( {1;2} \right);\,\,\overrightarrow {OB} = \left( {2;1} \right)\), biết \(\overrightarrow {MA} = 2\overrightarrow {MB} \). Khi đó độ dài vec-tơ \(\overrightarrow {OM} \) là:
A. 4. B. 1.
C. 3. D. 2.
2.5 : Phương trình \(\left( {mx + 2} \right)\left( {x + 1} \right) = \left( {mx + {m^2}} \right)x\) có nghiệm duy nhất khi m là :
A. \(m \ne – 1\) và \(m \ne 0\).
B. \(m \ne – 1\) và \(m \ne 2\)
C. \(m \ne 1\) và \(m \ne – 2\)
D. \(m \ne 2\) và \(m \ne 0\)
2.6 : Trong hệ trục \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\), tọa độ của vec-tơ \(\overrightarrow u = 3\overrightarrow j + 2\overrightarrow i \) là :
A. \(\overrightarrow u = \left( { – 2; – 3} \right)\).
B. \(\overrightarrow u = \left( {3;2} \right)\)
C.\(\overrightarrow u = \left( {2;3} \right)\)
D. \(\overrightarrow u = \left( { – 3;2} \right)\)
2.7 : Phương trình \(\left( {m + 2} \right){x^2} + 2\left( {3m – 2} \right)x + m + 2 = 0\) có nghiệm kép \(x = 1\) khi giá trị m là :
A. 2. B. 1.
C. 0. D. -1.
2.8 : Parabol \(y = – 4x – 2{x^2}\) có đỉnh là :
A. \(I\left( { – 1;2} \right)\)
B. \(I\left( {1;6} \right)\)
C. \(I\left( { – \dfrac{1}{4};\dfrac{7}{8}} \right)\).
D. \(I\left( {\dfrac{1}{4}; – \dfrac{9}{8}} \right)\).
2.9 : Tổng \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} \) bằng
A. \(\overrightarrow {MP} \). B. \(\overrightarrow {MR} \).
C. \(\overrightarrow {MN} \). D. \(\overrightarrow {PR} \).
3.0 : Parabol \(y = a{x^2} + bx + 2\) đi qua điểm \(M\left( {1; – 1} \right)\) và có trục đối xứng \(x = 2\)là:
A. \(y = {x^2} – 4x + 2\)
B. \(y = 2{x^2} + x + 2\)
C. \(y = – {x^2} + 2x + 2\)
D. \(y = {x^2} – 3x + 2\)
B. TỰ LUẬN (4đ)
1. (2đ). Cho phương trình \({x^2} – 2\left( {m – 1} \right)x + m – 3 = 0\), với m là tham số thực.
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt.
b) Tìm m để phương trình trên có hai nghiệm \({x_1};{x_2}\) thỏa mãn điều kiện \(x_1^2 + x_2^2 = 10\).
2. (1,5đ). Cho hình thang vuông ABCD, đường cao \(AB = 2a\), đáy lớn \(BC = 3a\), đáy nhỏ \(AD = a\).
1) Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CD} ;\,\,\overrightarrow {BD} .\overrightarrow {BC} \).
2) Gọi I là trung điểm CD. Tính góc của AI và BD.
3. (0,5đ).
Cho các số thực không âm a, b. Chứng minh rằng: \(\left( {{a^2} + b + \dfrac{3}{4}} \right)\left( {{b^2} + a + \dfrac{3}{4}} \right)\)\(\, \ge \left( {2a + \dfrac{1}{2}} \right)\).

A. TRẮC NGHIỆM (6đ)
| 1. B | 2. A | 3. A | 4. B | 5. A |
| 6. B | 7. A | 8. D | 9. C | 10. C |
| 11. A | 12. B | 13. C | 14. C | 15. B |
| 16. A | 17. A | 18. D | 19. A | 20. C |
| 21. B | 22. A | 23. C | 24. C | 25. B |
| 26. C | 27. C | 28. C | 29. C | 30. A |
B. TỰ LUẬN (4đ)
1. a) Ta có: \(\Delta ‘ = {\left( {m – 1} \right)^2} – \left( {m – 3} \right) \)\(\,= {m^2} – 3m + 4 \)\(\,= {\left( {m – \dfrac{3}{2}} \right)^2} + \dfrac{7}{4} > 0,\,\,\forall m\)
\( \Rightarrow \) Phương trình luôn có hai nghiệm phân biệt.
b) Theo Vi – et, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m – 2\\{x_1}.{x_2} = m – 3\end{array} \right.\)
Ta có:
\(\eqalign{
& x_1^2 + x_2^2 = 10\cr& \Leftrightarrow {\left( {{x_1} + {\rm{ }}{x_2}} \right)^2} – 2{x_1}.{x_2} = 10 \cr
& \Leftrightarrow {\left( {2m – 2} \right)^2} – 2.\left( {m – 3} \right) = 10 \cr
& \Leftrightarrow 4{m^2} – 10m = 0 \Leftrightarrow \left[ \matrix{
m = 0 \hfill \cr
m = \dfrac{5}{2} \hfill \cr} \right. \cr} \)
Kết luận: \(m \in \left\{ {0;\dfrac{5}{2}} \right\}\).
2.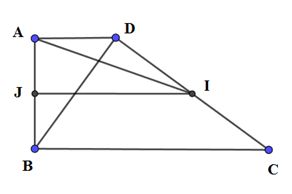
1) Ta có:
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AD} } \right)\\ = \overrightarrow {AB} .\overrightarrow {CB} + \overrightarrow {AB} .\overrightarrow {BA} + \overrightarrow {AB} .\overrightarrow {AD} \\ = 0 – A{B^2} + 0 = – {\left( {2a} \right)^2} = – 4{a^2}\end{array}\)
\(\begin{array}{l}\overrightarrow {BD} .\overrightarrow {BC} = \left( {\overrightarrow {BA} + \overrightarrow {AD} } \right).\overrightarrow {BC} \\ = \overrightarrow {BA} .\overrightarrow {BC} + \overrightarrow {AD} .\overrightarrow {BC} \\ = 0 + AD.BC.\cos \left( {\overrightarrow {AD} ;\overrightarrow {BC} } \right)\\ = a.3a.\cos 0^\circ = 3{a^2}\end{array}\)
2) Gọi J là trung điểm của AB \( \Rightarrow IJ\) là đường trung bình của hình thang ABCD
\( \Rightarrow IJ = \dfrac{{AD + BC}}{2} = \dfrac{{a + 3a}}{2} = 2a\) và \(IJ \bot AB\)
Ta có:
\(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {BD} = \left( {\overrightarrow {AJ} + \overrightarrow {JI} } \right).\left( {\overrightarrow {BA} + \overrightarrow {AD} } \right)\\ = \overrightarrow {AJ} .\overrightarrow {BA} + \overrightarrow {JI} .\overrightarrow {BA} + \overrightarrow {AJ} .\overrightarrow {AD} + \overrightarrow {JI} .\overrightarrow {AD} \\ = – \dfrac{1}{2}.{\left( {\overrightarrow {AB} } \right)^2} + 0 + 0 + JI.AD.\cos 0^\circ \\ = – \dfrac{1}{2}.{\left( {2a} \right)^2} + 2a.a.1 = 0\\ \Rightarrow AI \bot BD \Rightarrow \left( {\widehat {AI;BD}} \right) = 90^\circ \end{array}\)
3. Ta có:
\(\begin{array}{l}{a^2} + b + \dfrac{3}{4} = {a^2} + \dfrac{1}{4} + b + \dfrac{1}{2}\mathop \ge \limits^{Co\,si} 2\sqrt {{a^2}.\dfrac{1}{4}} + b + \dfrac{1}{2} = a + b + \dfrac{1}{2}\\{b^2} + a + \dfrac{3}{4} = {b^2} + \dfrac{1}{4} + a + \dfrac{1}{2}\mathop \ge \limits^{Co\,si} 2\sqrt {{b^2}.\dfrac{1}{4}} + a + \dfrac{1}{2} = a + b + \dfrac{1}{2}\\ \Rightarrow \left( {{a^2} + b + \dfrac{3}{4}} \right)\left( {{b^2} + a + \dfrac{3}{4}} \right) \ge {\left( {a + b + \dfrac{1}{2}} \right)^2}\end{array}\)
Mà \({\left( {a + b + \dfrac{1}{2}} \right)^2} = {\left( {a + \dfrac{1}{4} + b + \dfrac{1}{4}} \right)^2} \ge 4\left( {a + \dfrac{1}{4}} \right)\left( {b + \dfrac{1}{4}} \right) \)\(\,= \left( {2a + \dfrac{1}{2}} \right)\left( {2b + \dfrac{1}{2}} \right)\)
\( \Rightarrow \)\(\left( {{a^2} + b + \dfrac{3}{4}} \right)\)\(\left( {{b^2} + a + \dfrac{3}{4}} \right)\)\( \ge \)\(\left( {2a + \dfrac{1}{2}} \right)\)\(\left( {2b + \dfrac{1}{2}} \right)\)
Dấu “=” xảy ra khi \(a = b\).






