I – PHẦN TRẮC NGHIỆM (5đ)
1. : Đồ thị sau đây là của hàm số nào?
A. \(y = {x^2} – 4x – 3\)
B. \(y = – {x^2} + 4x\)
C. \(y = {x^2} + 4x – 3\)
D. \(y = – {x^2} + 4x – 3\)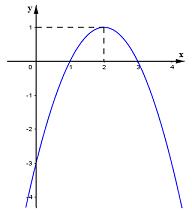 
2. : Trong mặt phẳng tọa độ Oxy cho các vectơ \(\overrightarrow a = \left( {1; – 3} \right);\,\,\overrightarrow b = \left( {5;2} \right)\). Tọa độ vectơ \(\overrightarrow x = 2\overrightarrow a – 3\overrightarrow b \) là:
A. \(\overrightarrow x = \left( { – 12;13} \right)\)
B. \(\overrightarrow x = \left( {12;13} \right)\)
C. \(\overrightarrow x = \left( { – 13; – 12} \right)\)
D. \(\overrightarrow x = \left( { – 13;12} \right)\)
3. : Điều kiện xác định của phương trình \(x – 1 + \dfrac{1}{{x – 1}} = \dfrac{x}{{\sqrt x }}\) là:
A. \(x \ge 0;\,\,x \ne 1\)
B. \(x \ge 1\)
C. \(x > 1\)
D. \(x > 0;\,\,x \ne 1\)
4. : Cho hàm số \(y = \left| {x – 3} \right|\). Chọn khẳng định đúng trong các khẳng định sau về hàm số
A. Hàm số chẵn
B. Hàm số đồng biến trên R
C. Giá trị nhỏ nhất của hàm số là \(y = 0\)
D. Hàm số nghịch biến trên R.
5. : Số giao điểm của 2 đồ thị hàm số \(\left( {{P_1}} \right):\,\,y = – {x^2} + x\) và \(\left( {{P_2}} \right):\,\,y = {x^2} – 2x – 3\) là :
A. 1 B. 0
C. 3 D. 2
6. : Trong mặt phẳng tọa độ Oxy cho 2 điểm \(A\left( {2; – 5} \right)\) và \(B\left( { – 1;3} \right)\). Tọa độ vectơ \(\overrightarrow {AB} \) là:
A. \(\overrightarrow {AB} = \left( {1; – 2} \right)\)
B. \(\overrightarrow {AB} = \left( { – 3;8} \right)\)
C. \(\overrightarrow {AB} = \left( {3; – 8} \right)\)
D. \(\overrightarrow {AB} = \left( { – 2; – 15} \right)\)
7. : Số nghiệm của phương trình \(\dfrac{{{x^2} + 6}}{{x – 2}} = \dfrac{{5x}}{{x – 2}}\) là :
A. 3 B. 2
C. 3 D. 0
8. : Số nghiệm của phương trình \(x\sqrt {x – 2} = \sqrt {2 – x} \) là:
A. 1 B. 2
C. 3 D. 0
9. : Tìm tất cả các giá trị của m để hàm số \(y = \sqrt {x – 1} + \sqrt {m – x} \) xác định trên tập \(\left( {1;3} \right)\) ? Đáp án đúng là :
A. \(1 \le m \le 3\)
B. \(m \ge 3\)
C. \(m < 1\)
D. \(m > 3\)
1.0 : Cho parabol \(\left( P \right):\,\,y = – 3{x^2} + 9x + 2\) và các điểm \(M\left( {2;8} \right);\,\,N\left( {3;56} \right)\). Chọn khẳng định đúng:
A. \(M \in \left( P \right);\,\,N \in \left( P \right)\)
Advertisements (Quảng cáo)
B. \(M \notin \left( P \right);\,\,N \notin \left( P \right)\)
C. \(M \notin \left( P \right);\,\,N \in \left( P \right)\)
D. \(M \in \left( P \right);\,\,N \notin \left( P \right)\)
1.1 : Trục đối xứng của đồ thị hàm số \(y = {x^2} – 4x + 3\) là đường thẳng :
A. \(x = – 2\)
B. \(y = – 4\)
C. \(y = 2\)
D. \(x = 2\)
1.2 : Cho hàm số \(y = {x^2} – 4x + 7\). Chọn khẳng định đúng ?
A. Hàm số đồng biến trên R
B. Hàm số đồng biến trên khoảng \(\left( { – 2; + \infty } \right)\)
C. Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
D. Hàm số nghịch biến trên khoảng \(\left( { – 2; + \infty } \right)\)
1.3 : Số giao điểm của đồ thị hàm số \(y = 2{x^2} + x – 5\) với trục hoành là:
A. 0 B. 1
C. 2 D. 3
1.4 : Trong mặt phẳng tọa độ Oxy cho \(A\left( {2;5} \right);\,\,B\left( {1;3} \right);\,\,C\left( {5; – 1} \right)\). Tọa độ trọng tâm G của tam giác ABC là:
A. \(G\left( {8;7} \right)\)
B. \(G\left( {\dfrac{8}{3};\dfrac{7}{3}} \right)\)
C. \(G\left( { – \dfrac{8}{3}; – \dfrac{7}{3}} \right)\)
D. \(G\left( { – \dfrac{8}{3};\dfrac{7}{3}} \right)\)
1.5 : Tìm m để 3 đường thẳng \({d_1}:\,\,y = x + 1;\,\,{d_2}:\,\,y = 3x – 1;\)\(\,\,{d_3}:\,\,2mx – 4m\) đồng quy (cùng đi qua 1đ) ? Đáp án đúng là:
A. \(m = 1\) B. \(m = – 1\)
C. \(m = 0\) D. \(m \in \emptyset \)
1.6 : Trong mặt phẳng tọa độ Oxy cho hình thang ABCD có đáy lớn CD gấp đôi đáy nhỏ AB. Biết \(A\left( {1;1} \right);\,\,B\left( { – 1;2} \right);\,\,C\left( {0;1} \right)\). Tìm tọa độ điểm D ?
A. \(D\left( {4; – 1} \right)\)
B. \(D\left( { – 4; – 1} \right)\)
Advertisements (Quảng cáo)
C. \(D\left( {4;1} \right)\)
D. \(D\left( { – 4;1} \right)\)
1.7 : Hàm số nào dưới đây là hàm số lẻ trên tập xác định của nó ?
A. \(y = {x^3} – x + 1\)
B. \(y = {x^4} – 2{x^2} + 1\)
C. \(y = \left| {x + 1} \right| + \left| {x – 1} \right|\)
D. \(y = 2x – {x^3}\)
1.8 : Tìm m để đồ thị hàm số \(y = \left| {{x^2} – 3x + 1} \right|\) cắt đường thẳng \(y = m\) tại 4 điểm phân biệt ? Đáp án đúng là:
A. \(0 \le m \le \dfrac{5}{4}\)
B. \(0 < m < \dfrac{5}{4}\)
C. \(m > 0\)
D. \(m > \dfrac{5}{4}\)
1.9 : Tập nghiệm của phương trình \(\left( {{m^2} – 9} \right)x + 6 – 2m = 0\) trong trường hợp \({m^2} – 9 \ne 0\) là :
A. \(\left\{ {\dfrac{2}{{m + 3}}} \right\}\)
B. \(\left\{ {\dfrac{2}{{m – 3}}} \right\}\)
C. \(\emptyset \)
D. \(R\)
2.0 : Tập nghiệm của phương trình \(\sqrt {2x – 1} = x – 1\) là :
A. \(\left\{ {2 + \sqrt 2 } \right\}\)
B. \(\emptyset \)
C. \(\left\{ {2 + \sqrt 2 ;2 – \sqrt 2 } \right\}\)
D. \(\left\{ {2 – \sqrt 2 } \right\}\)
2.1 : Tìm m để hàm số \(y = \left( {m – \sqrt 5 } \right)x – 2\) nghịch biến trên R ?
A. \(m > \sqrt 5 \)
B. \(m \le \sqrt 5 \)
C. \(m \ge \sqrt 5 \)
D. \(m < \sqrt 5 \)
2.2 : Tìm m để hàm số \(y = \left( {m – 2} \right)x + 1\) là hàm số bậc nhất ?
A. \(m \ne 0;\,\,m \ne 2\)
B. \(m \ne 2\)
C. \(\forall m \in R\)
D. \(m \ne 0\).
2.3 : Tập xác định của hàm số \(y = \dfrac{{x – 3}}{{x + 2}}\) là :
A. \(R\)
B. \(\left( { – 2; + \infty } \right)\)
C. \(R\backslash \left\{ 2 \right\}\)
D. \(R\backslash \left\{ { – 2} \right\}\)
2.4 : Giá trị lớn nhất của hàm số \(y = – {x^2} + 2x + 3\) trên đoạn \(\left[ {2;3} \right]\) là :
A. 3 B. 4
C. 1 D. 6
2.5 : Trong mặt phẳng tọa độ Oxy cho 4 điểm \(A\left( {2;5} \right);\,\,B\left( {1;7} \right);\,\,C\left( {1;5} \right);\,\,D\left( {0;9} \right)\). Ba điểm nào sau đây thẳng hàng.
A. Ba điểm A, B, D
B. Ba điểm A, B, C
C. Ba điểm B, C, D
D. Ba điểm A, C, D
II – PHẦN TỰ LUẬN (5đ)
Bài 1 (1đ): Giải phương trình \(\sqrt {2{x^2} – 5x + 2} = x – 2\)
Bài 2 : Cho hệ phương trình \(\left\{ \begin{array}{l}2x – y + 1 = 0\\{x^2} – 3xy + {y^2} = 2x – 5 + {m^2}\end{array} \right.\)
a) (1đ) Giải hệ phương trình với \(m = 0\).
b) (0,5đ) Tìm m để hệ có nghiệm.
Bài 3 : Trong mặt phẳng tọa độ Oxy cho tam giác ABC với \(A\left( { – 1;1} \right);\,\,B\left( {3;1} \right);\,\,C\left( {2;4} \right)\).
a) (0,5đ) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) ?
b) (0,5đ) Tính \(\widehat {BAC}\).
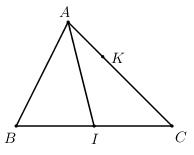
Bài 4 : Cho tam giác ABC. Gọi I là trung điểm của BC; K là điểm thuộc cạnh AC sao cho \(KC = 2AK\).
a) (1đ) Biểu diễn các vectơ \(\overrightarrow {AI} ;\,\,\overrightarrow {AK} ;\,\overrightarrow {KI} \) theo 2 vectơ \(\overrightarrow {AB;} \,\,\overrightarrow {AC} \).
b) (0;5đ) Xác định vị trí của M sao cho \(2M{A^2} + M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất.
I – PHẦN TRẮC NGHIỆM
|
1. D |
2. C |
3. D |
4. C |
5. D |
|
6. B |
7. C |
8. A |
9. B |
10. D |
|
11. D |
12. C |
13. C |
14. B |
15. B |
|
16. A |
17. D |
18. B |
19. A |
20. A |
|
21. D |
22. B |
23. D |
24. A |
25. A |
II – PHẦN TỰ LUẬN (5đ)
Bài 1: Phương trình có nghiệm duy nhất \(x = 2\).
Bài 2: a) \(S = \left\{ {\left( {2;5} \right);\left( { – 3; – 5} \right)} \right\}\).
b) \( – \dfrac{5}{2} \le m \le \dfrac{5}{2}\).
Bài 3: a) \( \overrightarrow {AB} .\overrightarrow {AC} = 12\)
b) \(\widehat {BAC} = {45^0}\)
Bài 4: a) \(\overrightarrow {AI} = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AC} \).
\(\overrightarrow {AK} = \dfrac{1}{3}\overrightarrow {AC} \).
\(\overrightarrow {KI} = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{6}\overrightarrow {AC} \)
b) \(2M{A^2} + M{B^2} + M{C^2}\) nhỏ nhất khi và chỉ khi M là trung điểm của AI.
