
I. TRẮC NGHIỆM (gồm 40 câu, 8 điểm, thời gian làm 75 phút)
1. : Phương trình \(\left| {x – 2} \right| = \left| {3x – 1} \right|\)có tập nghiệm là:
A. \(S = \left\{ { – \dfrac{1}{2};\dfrac{3}{4}} \right\}\).
B. \(S = \left\{ {\dfrac{3}{4}} \right\}\).
C. \(S = \left\{ { – \dfrac{1}{2}} \right\}\).
D. \(S = \mathbb{R}\).
2. : Cho phương trình \(\left| {x – 3m + 1} \right| = \left| {\left( {m + 1} \right)x – 3} \right|\). Khẳng định nào dưới đây đúng?
A. Khi \(m = 0\) phương trình vô nghiệm.
B. Khi \(m = – 2\) phương trình có nghiệm duy nhất.
C. Khi \(m \ne 0\) và \(m \ne – 2\) phương trình có hai nghiệm.
D. Khi \(m \ne 0\) phương trình có nghiệm duy nhất.
3. : Cho phương trình \(\dfrac{{3m\left( {x – 1} \right)}}{{x + 1}} = 5m + 1\). Khẳng định nào dưới đây đúng?
A. Khi \(m \ne – \dfrac{1}{8}\) phương trình có nghiệm bằng 0.
B. Khi \(m \ne – \dfrac{1}{2}\) phương trình có nghiệm duy nhất \(x = \dfrac{{ – 8m – 1}}{{2m + 1}}\).
C. Khi \(\left\{ \begin{array}{l}m \ne – \dfrac{1}{2}\\m \ne 0\end{array} \right.\) phương trình có nghiệm duy nhất \(x = \dfrac{{ – 8m – 1}}{{2m + 1}}\).
D. Khi \(m = – \dfrac{1}{2}\) phương trình có tập nghiệm bằng \(S = \mathbb{R}\).
4. : Tập nghiệm của phương trình \({x^2} + 2\left| x \right| – 3 = 0\).
A. \(\left\{ { – 2;2} \right\}\). B. \(\left\{ { – 1;1} \right\}\).
C. \(\left\{ { – 1;2} \right\}\). D. \(\left\{ { – 2;1} \right\}\).
5. : Cho \(\Delta ABC\), tập hợp các điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {BC} } \right| = \dfrac{1}{2}\left| {\overrightarrow {MA} – \overrightarrow {MB} } \right|\) là:
A. Đường trung trực đoạn BC.
B. Đường tròn tâm I, bán kính \(R = \dfrac{{AB}}{2}\) với I là đỉnh hình bình hành ABIC.
C. Đường thẳng song song với BC.
D. Đường tròn tâm I, bán kính \(R = \dfrac{{AB}}{2}\) với I là đỉnh hình bình hành ABCI.
6. : Số nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y + xy = 11\\{x^2} + {y^2} + 3\left( {x + y} \right) = 28\end{array} \right.\) bằng
A. 4. B. 3.
C. 1. D. 2.
7. : Trong hệ trục tọa độ Oxy, cho \(A\left( {1;1} \right),\,B\left( { – 1;3} \right)\) và \(H\left( {0;1} \right)\). Tìm tọa độ điểm C sao cho H là trực tâm tam giác ABC.
A. \(C\left( { – 1;0} \right)\). B. \(C\left( {1;0} \right)\).
C. \(C\left( {0;1} \right)\). D. \(C\left( {0; – 1} \right)\).
8. : Cho \(\Delta ABC\) có trung tuyến AM, chọn khẳng định đúng trong các khẳng định sau:
A. \(\overrightarrow {AM} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
B. \(\overrightarrow {AM} = – \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\).
C. \(\overrightarrow {AM} = \dfrac{1}{2}\left( {\overrightarrow {AB} – \overrightarrow {AC} } \right)\).
D. \(\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {BM} \).
9. : Tìm điều kiện của m để phương trình \(2{x^2} – 4mx + 2{m^2} + m + 1 = 0\) có nghiệm.
A. \(m > 1\). B. \(m \le – 1\).
C. \(m < – 1\). D. \(m = 1\).
1.0 : Xác định hàm số \(f\left( x \right)\) biết đồ thị của nó là đường thẳng đi qua hai điểm \(A\left( {1;5} \right),\,\,B\left( {0;2} \right)\).
A. \(f\left( x \right) = 3x + 2\).
B. \(f\left( x \right) = – 3x – 2\).
C. \(f\left( x \right) = – 3x + 2\).
D. \(f\left( x \right) = 3x – 2\).
1.1 : Cho góc \(x\) thỏa mãn \(90^\circ < x < 180^\circ \). Đặt \(P = \sin \,x\cos x\). Ta có mệnh đề đúng là:
A. \(P = 0\). B. \(P > 0\).
C. \(P < 0\). D. \(P > 1\).
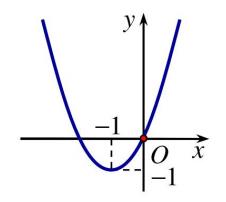
1.2 : Đồ thị trong hình là đồ thị hàm số nào trong các hàm số sau:
A. \(y = {x^2} – 2x + 2\).
B. \(y = {x^2} + 2x\).
C. \(y = – {x^2} + 2x\).
D. \(y = – {x^2} – 2x – 2\).
1.3 : Cho hàm số \(y = \left( {{m^2} – 4} \right)x + 2m – 1\). Xác định m để hàm số đồng biến trên R.
A. \(\left[ \begin{array}{l}m < 2\\m > – 2\end{array} \right.\).
B. \(\left[ \begin{array}{l}m > 2\\m < – 2\end{array} \right.\).
C. \(\left\{ \begin{array}{l}m > 2\\m < – 2\end{array} \right.\).
D. \(\left\{ \begin{array}{l}m < 2\\m > – 2\end{array} \right.\).
1.4 : Tập giá trị của hàm số \(y = \left| {3 + x} \right| – 1\) là:
A. \(\mathbb{R}\).
B. \(\left[ { – 1; + \infty } \right)\).
C. \(R{\rm{\backslash }}\left\{ 1 \right\}\).
Advertisements (Quảng cáo)
D. \(\left( { – \infty ;1} \right]\).
1.5 : Khẳng định nào sau đây sai?
A. Nếu \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) thì ABCD là hình bình hành.
B. Nếu \(O\) là trung điểm của AB thì với mọi điểm M ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MO} \).
C. Nếu \(G\)là trọng tâm tam giác ABC thì \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} \).
D. Với ba điểm bất kì \(I,\,J,\,K\) ta có: \(\overrightarrow {IJ} + \overrightarrow {JK} = \overrightarrow {IK} \).
1.6 : Số nghiệm nguyên của phương trình: \(\sqrt {x – 3} + 5 = \sqrt {7 – x} + x\) là:
A. 3. B. 0.
C. 1. D. 2.
1.7 : Trong mặt phẳng Oxy cho \(A\left( {4;6} \right),\,B\left( {1;4} \right)\) và \(C\left( {7;\dfrac{3}{2}} \right)\). Ta có khẳng định nào sau đây là đúng?
A. \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) < 90^\circ \).
B. \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = 90^\circ \).
C. \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = 180^\circ \).
D. \(\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = 0^\circ \).
1.8 : Cho hai điểm phân biệt A và B . Điều kiện cần và đủ để điểm I là trung điểm của đoạn AB là:
A. \(IA = IB\).
B. \(\overrightarrow {AI} = \overrightarrow {BI} \).
C. \(\overrightarrow {IA} = \overrightarrow {IB} \).
D. \(\overrightarrow {IA} = – \overrightarrow {IB} \).
1.9 : Xác định tập nghiệm của phương trình : \({x^2} – \left( {3m + 1} \right)x + 3m = 0\).
A. \(S = \left\{ {1; – 3m} \right\}\).
B. \(S = \left\{ { – 1;3m} \right\}\).
C. \(S = \left\{ {1;3m} \right\}\).
D. \(S = \left\{ { – 1; – 3m} \right\}\).
2.0 : Xác định phương trình của Parabol có đỉnh \(I\left( {0; – 1} \right)\) và đi qua điểm \(A\left( {2;3} \right)\).
A. \(y = {x^2} + 1\).
B. \(y = {\left( {x – 1} \right)^2}\).
C. \(y = {\left( {x + 1} \right)^2}\).
D. \(y = {x^2} – 1\).
2.1 : Cho phương trình \(\left( {{m^2} – 1} \right)x + m + 1 = 0\). Khẳng định nào dưới đây là sai?
A. Khi \(m \ne \pm 1\) phương trình có nghiệm duy nhất.
B. Khi \(m = 1\) phương trình có tập nghiệm\(S = \emptyset \).
C. Khi \(m = – 1\) phương trình có tập nghiệm\(S = R\).
D. Khi \(m = \pm 1\) phương trình vô nghiệm.
2.2 : Hàm số \(y = 2{x^2} + 16x – 25\) đồng biến trên khoảng:
A. \(\left( { – 4; + \infty } \right)\).
B. \(\left( { – \infty ;8} \right)\).
C. \(\left( { – \infty ; – 4} \right)\).
D. \(\left( { – 6; + \infty } \right)\).
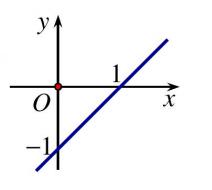
2.3 : Đồ thị trong hình là đồ thị của hàm số nào dưới đây?
A. \(y = x + 1\).
Advertisements (Quảng cáo)
B. \(y = – x + 1\).
C. \(y = x – 1\).
D. \(y = – x – 1\).
2.4 : Cho tập hợp \(A = \left( { – \infty ;3} \right],\,\,\,B = \left( {2; + \infty } \right)\). Khi đó, tập \(B \cup A\) là:
A. \(\left( {2;3} \right]\).
B. \(\left( { – 3;2} \right]\).
C. \(\mathbb{R}\).
D. \(\emptyset \).
2.5 : Cho tập hợp \(A = \left\{ {a;\,b;\,c;\,d} \right\}\). Số tập con gồm hai phần tử của A là:
A. 5. B. 6.
C. 4. D. 7.
2.6 : Cho tập hợp \(A = \left\{ {x \in N|x \le 5} \right\}\). Tập A được viết dưới dạng liệt kê các phần tử là:
A. \(A = \left\{ {0;1;2;4;5} \right\}\).
B. \(A = \left\{ {1;2;3;4;5} \right\}\).
C. \(A = \left\{ {0;1;2;3;4;5} \right\}\).
D. \(A = \left\{ {0;1;2;3;4} \right\}\).
2.7 : Chuẩn bị được nghỉ hè, một lớp có 45 học sinh bàn nhau chọn một trong hai địa điểm để cả lớp cùng đi tham quan du lịch. Do sự lựa chọn của các bạn không được tập trung và thống nhất vào một địa điểm nào, lớp trưởng đã lấy biểu quyết bằng giơ tay. Kết quả: hai lần số bạn chọn đi Tam Đảo thì ít hơn ba lần số bạn chọn đi Hạ Long là 3 bạn và có 9 bạn chọn đi địa điểm khác. Với nghiên tắc số ít hơn phải theo số đông hơn thì họ sẽ đi địa điểm nào?
A. Địa điểm khác.
B. Tạm hoãn để bàn lại.
C. Tam Đảo.
D. Hạ Long.
2.8 : Cho tập hợp \(A = \left[ { – 2;3} \right],\,\,B\left( {1;5} \right]\). Khi đó, tập \(A\backslash B\) là:
A. \(\left[ { – 2;1} \right)\). B. \(\left( { – 2; – 1} \right)\).
C. \(\left( { – 2;1} \right]\). D. \(\left[ { – 2;1} \right]\).
2.9 : Xác định tập nghiệm của phương trình \(\sqrt {4x – 1} = x – 2\).
A. \(S = \left\{ {4 + \sqrt {11} } \right\}\).
B. \(S = \left\{ {4 – \sqrt {11} } \right\}\).
C. \(S = \left\{ {4 + \sqrt {11} ;4 – \sqrt {11} } \right\}\).
D. \(S = \emptyset \).
3.0 : Số nghiệm của phương trình: \(2x + \dfrac{1}{{\sqrt {x + 1} }} = – {x^2} + \dfrac{1}{{\sqrt {x + 1} }}\)là:
A. 0. B. 1.
C. 2. D. 3.
3.1 : Cho tập hợp \(A = \left[ {m;m + 2} \right],\,\,B = \left[ { – 1;2} \right]\). Điều kiện của m để \(A \subset B\) là:
A. \(1 \le m \le 2\).
B. \( – 1 \le m \le 0\).
C. \(m \le – 1\) hoặc \(m \ge 0\).
D. \(m < – 1\) hoặc \(m > 2\).
3.2 : Hệ phương trình \(\left\{ \begin{array}{l}mx + y = m + 1\\2x – \left( {m – 1} \right)y = 3\end{array} \right.\) là hệ hai phương trình bậc nhất hai ẩn khi có
A. \(m \in R\).
B. \(m \in R{\rm{\backslash }}\left\{ { – 1;0;1} \right\}\).
C. \(m \in R{\rm{\backslash }}\left\{ 0 \right\}\).
D. \(m \in R{\rm{\backslash }}\left\{ {0;1} \right\}\).
3.3 : Cho hình chữ nhật ABCD có cạnh \(AB = a,\,\,BC = 2a\), khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|\) bằng:
A. \(a\sqrt 3 \). B. \(a\).
C. \(3a\). D. \(a\sqrt 5 \).
3.4 : Giải hệ phương trình \(\left\{ \begin{array}{l}\sqrt 3 x + \sqrt 2 y = – 1\\2\sqrt 2 x + \sqrt 3 y = 0\end{array} \right.\) ta có nghiệm là:
A. \(\left( { – \sqrt 3 ; – 2\sqrt 2 } \right)\).
B. \(\left( { – \sqrt 3 ;2\sqrt 2 } \right)\).
C.\(\left( {\sqrt 3 ;2\sqrt 2 } \right)\).
D. \(\left( {\sqrt 3 ; – 2\sqrt 2 } \right)\).
3.5 : Giá trị lớn nhất của hàm số \(y = – {x^2} + 4x – 1\) là:
A. -2. B. -3.
C. 3. D. 2.
3.6 : Cho tam giác đều cạnh a. Mệnh đề nào sau đây đúng?
A. \(\overrightarrow {AB} \) cùng hướng với \(\overrightarrow {BC} \).
B. \(\left| {\overrightarrow {AC} } \right| = \overrightarrow {BC} \).
C. \(\left| {\overrightarrow {AB} } \right| = a\).
D. \(\overrightarrow {AC} = a\).
3.7 : Cho tam giác ABC vuông tại A, có số đo góc B là \(60^\circ \) và \(AB = a\). Kết quả nào sau đây là sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} = 0\).
B. \(\overrightarrow {CA} .\overrightarrow {CB} = 3{a^2}\).
C. \(\overrightarrow {AB} .\overrightarrow {BC} = – {a^2}\).
D. \(\overrightarrow {AC} .\overrightarrow {CB} = – 3\sqrt 2 a\).
3.8 : Tọa độ đỉnh của parabol \(y = {x^2} – 2x + 4\) là:
A. \(I\left( {1; – 3} \right)\).
B.\(I\left( { – 1; – 3} \right)\).
C. \(I\left( { – 1;3} \right)\).
D. \(I\left( {1;3} \right)\).
3.9 : Cho tam giác ABC, có bao nhiêu điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3\)?
A. 3. B. 2.
C. 1. D. Vô số.
4.0 : Tập xác định của hàm số \(y = \sqrt {x + 2} + \dfrac{{{x^3}}}{{4\left| x \right| – 3}}\) là:
A. \(D = \left[ { – 2; + \infty } \right)\).
B. \(D = \left[ { – 2; + \infty } \right){\rm{\backslash }}\left\{ { – \dfrac{3}{4};\dfrac{3}{4}} \right\}\).
C. \(D = \left\{ { – \dfrac{3}{4};\dfrac{3}{4}} \right\}\).
D. \(D = R{\rm{\backslash }}\left\{ { – \dfrac{3}{4};\dfrac{3}{4}} \right\}\).
II. TỰ LUẬN (gồm 2 câu, 2 điểm, thời gian làm 15 phút)
1. (1,0đ)
a) Tìm m để phương trình \({x^2} + 2x + m = 0\) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa \(x_1^2 + x_2^2 = 6\).
b) Giải phương trình: \(\sqrt {{x^2} + 2x – 6} = 2x – 3\).
2. (1,0đ)
a) Cho biết \(\sin \alpha = \dfrac{1}{4}\). Hãy tính \(\cot \alpha \)? (0,5đ).
b) Trong mặt phẳng Oxy cho bốn điểm không thẳng hàng: \(A\left( {3;4} \right),\,B\left( {4;1} \right),\,C\left( {2; – 3} \right),\,D\left( { – 1;6} \right)\). Chứng minh rằng: ABCD là tứ giác nội tiếp được một đường tròn. (0,5đ).

I. PHẦN TRẮC NGHIỆM
| 1. A | 11. C | 21. D | 31. B |
| 2. B | 12. B | 22. A | 32. A |
| 3. C | 13. B | 23. C | 33. D |
| 4. B | 14. B | 24. C | 34. D |
| 5. D | 15. A | 25. B | 35. C |
| 6. A | 16. A | 26. B | 36. C |
| 7. A | 17. B | 27. C | 37. D |
| 8. A | 18. D | 28. D | 38. D |
| 9. B | 19. C | 29. A | 39. D |
| 10. A | 20. D | 30. B | 40. B |
II. TỰ LUẬN (gồm 2 câu, 2 điểm, thời gian làm 15 phút)
1. a) Để phương trình \({x^2} + 2x + m = 0\) có 2 nghiệm phân biệt thì \(\Delta ‘ > 0 \Leftrightarrow 1 – m > 0 \Leftrightarrow m < 1\)
Theo Vi – ét, ta có: \({x_1} + {x_2} = \dfrac{{ – 2}}{1} = – 2,\,\,\,{x_1}{x_2} = \dfrac{m}{1} = m\)
Theo đề bài:
\(\begin{array}{l}x_1^2 + x_2^2 = 6\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} – 2{x_1}{x_2} = 6\\ \Leftrightarrow {\left( { – 2} \right)^2} – 2m = 6\\ \Leftrightarrow 4 – 2m = 6\\ \Leftrightarrow 2m = – 2 \Leftrightarrow m = – 1\end{array}\)
Kết luận: \(m = – 1\) thỏa mãn yêu cầu bài toán.
b) \(\begin{array}{l}\sqrt {{x^2} + 2x – 6} = 2x – 3\\ \Leftrightarrow \left\{ \begin{array}{l}2x – 3 \ge 0\\{x^2} + 2x – 6 = {\left( {2x – 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\{x^2} + 2x – 6 = 4{x^2} – 12x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\3{x^2} – 14x + 15 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{5}{3}\end{array} \right.\,\,\left( {tm} \right)\end{array}\)
Vậy, phương trình đã cho có tập nghiệm \(S = \left\{ {3;\dfrac{5}{3}} \right\}\).
2. (1,0đ)
a) Ta có:
\(\begin{array}{l}1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow 1 + {\cot ^2}\alpha = \dfrac{1}{{{{\left( {\dfrac{1}{4}} \right)}^2}}}\\ \Leftrightarrow {\cot ^2}\alpha = 15\\ \Leftrightarrow \left[ \begin{array}{l}\cot \alpha = \sqrt {15} \\\cot \alpha = – \sqrt {15} \end{array} \right.\end{array}\).
b) \(\overrightarrow {AB} = \left( {1; – 3} \right),\,\overrightarrow {AD} = \left( { – 4;2} \right),\)\(\,\,\overrightarrow {CB} = \left( {2;4} \right),\,\overrightarrow {CD} = \left( { – 3;9} \right)\)
\(\begin{array}{l}\cos \widehat {BAD} = \cos \left( {\overrightarrow {AB} ;\overrightarrow {AD} } \right) = \dfrac{{1.\left( { – 4} \right) + \left( { – 3} \right).2}}{{\sqrt {{1^2} + {{\left( { – 3} \right)}^2}} .\sqrt {{{\left( { – 4} \right)}^2} + {2^2}} }} = – \dfrac{1}{{\sqrt 2 }} \\\Rightarrow \widehat {BAD} = 135^\circ \\\cos \widehat {BCD} = \cos \left( {\overrightarrow {CB} ;\overrightarrow {CD} } \right) = \dfrac{{2.\left( { – 3} \right) + 4.9}}{{\sqrt {{2^2} + {4^2}} .\sqrt {{{\left( { – 3} \right)}^2} + {9^2}} }} = \dfrac{1}{{\sqrt 2 }}\\ \Rightarrow \widehat {BCD} = 45^\circ \end{array}\)
\( \Rightarrow \widehat {BAD} + \widehat {BCD} = 135^\circ + 45^\circ = 180^\circ \)
\( \Rightarrow \) ABCD là tứ giác nội tiếp được một đường tròn (đpcm).





