Thi kì 1 môn Toán học lớp 8: Tìm điều kiện xác định của biểu thức P?

Bài 1.Phân tích đa thức \({x^2} + 4{y^2} + 4xy – 16\) thành nhân tử.

Bài 2.Thực hiện phép tính: \({{2x + 6} \over {3{x^2} – x}}:{{{x^2} + 3x} \over {1 – 3x}}.\)

Bài 3.Cho biểu thức \(P = {{8{x^3} – 12{x^2} + 6x – 1} \over {4{x^2} – 4x + 1}}.\)

a) Tìm điều kiện xác định của biểu thức P.

b)Chứng minh rằng mọi giá trị của x nguyên thì P nguyên.

Bài 4.Chứng minh rằng \(\left( {{x \over {{x^2} – 36}} – {{x – 6} \over {{x^2} + 6x}}} \right):{{2x – 6} \over {{x^2} + 6x}} + {x \over {6 – x}} =  – 1.\)

Bài 5.Tìm chiều cao AH của hình thang ABCD \(\left( {AB\parallel CD} \right)\) biết AB = 7cm, đường trung bình MN = 9cm và diện tích hình thang bằng \(45c{m^2}\).

Bài 6.Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right).\) Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.

a)Chứng minh tư giác AMIN là hình chữ nhật.

b)Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.

c)Cho AC = 20cm, BC = 25cm. Tính diện tích \(\Delta ABC.\)

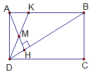
d)Đường thẳng BN cắt cạnh DC tại K. Chứng minh: \({{DK} \over {DC}} = {1 \over 3}.\)

Bài 1. \({x^2} + 4{y^2} + 4xy – 16\)

\(= {\left( {x + 2y} \right)^2} – 16\)

\(= \left( {x + 2y – 4} \right)\left( {x + 2y + 4} \right).\)

Bài 2. Điều kiện: \(x \ne 0;x \ne  \pm {1 \over 3}.\)

\({{2x + 6} \over {3{x^2} – x}}:{{{x^2} + 3x} \over {1 – 3x}} = {{2\left( {x + 3} \right)} \over {x\left( {3x – 1} \right)}}.{{1 – 3x} \over {x\left( {x + 3} \right)}} = {{ – 2\left( {3x – 1} \right)} \over {x\left( {3x – 1} \right)}} =  – {2 \over x}.\)

Bài 3. a)Điều kiện: \(4{x^2} – 4x + 1 \ne 0\) hay \({\left( {2x – 1} \right)^2} \ne 0\) hay \(2x – 1 \ne 0\)

Vậy \(x \ne {1 \over 2}.\)

b) Ta có: \(P = {{{{\left( {2x – 1} \right)}^3}} \over {{{\left( {2x – 1} \right)}^2}}} = 2x – 1.\)

Vậy với mọi \(x \in Z \Rightarrow 2x – 1 \in Z\) hay \(x \in Z\)

Bài 4. Điều kiện: \(x \ne  \pm 6;x \ne 0.\) Biến đổi vế trái (VT), ta được:

\(VT = {{{x^2} – {{\left( {x – 6} \right)}^2}} \over {x\left( {{x^2} – 36} \right)}}:{{2\left( {x – 3} \right)} \over {x\left( {x + 6} \right)}} + {x \over {6 – x}} = {{12x – 36} \over {x\left( {{x^2} – 36} \right)}}.{{x\left( {x + 6} \right)} \over {2\left( {x – 3} \right)}} + {x \over {6 – x}}\)

\( = {{12\left( {x – 3} \right)} \over {2\left( {x – 6} \right)\left( {x – 3} \right)}} + {x \over {6 – x}} = {6 \over {x – 6}} – {x \over {x – 6}} = {{6 – x} \over {x – 6}} =  – 1\) (đpcm)

Bài 5.

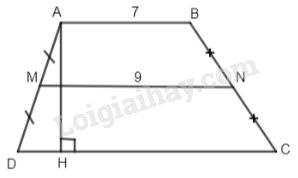
Ta có:  \(MN = {{AB + CD} \over 2} \Rightarrow 2MN = AB + CD\)

\( \Rightarrow CD = 2MN – AB = 2.9 – 7 = 11\left( {cm} \right)\)

Lại có: \({S_{ABCD}} = {{\left( {AB + CD} \right)AH} \over 2}\)

\( \Rightarrow 2{S_{ABCD}} = \left( {AB + CD} \right).AH\)

\( \Rightarrow AH = {{2{S_{ABCD}}} \over {AB + CD}} = {{2.45} \over {7 + 11}} = 5\left( {cm} \right)\)

Bài 6.

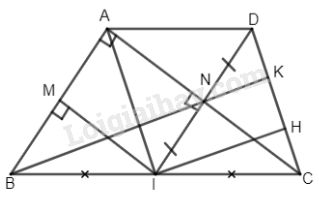
a) Ta có AMIN là hình chữ nhật (có 3 góc vuông)

b) \(\Delta ABC\) vuông có AI là trung tuyến nên \(AI = IC = {1 \over 2}BC\)

Do đó \(\Delta AIC\) cân có đường cao IN đồng thời là trung tuyến

\( \Rightarrow NA = NC.\)

Lại có: ND = NI (t/c đối xứng) nên ADCI là hình bình hành có \(AC \bot ID\) (gt). Do đó ADCI là hình thoi.

c) Ta có: \(A{B^2} = B{C^2} – A{C^2}\) (định lý Py – ta – go)

                      \( = {25^2} – {20^2} \Rightarrow AB = \sqrt {225}  = 15\left( {cm} \right)\)

Vậy \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.15.20 = 150\left( {c{m^2}} \right)\) .

d) Kẻ \(IH\parallel BK\) ta có IH là đường trung bình của \(\Delta BKC\)

\( \Rightarrow H\) là trung điểm của CK hay KH = HC (1)

Xét \(\Delta DIH\) có N là trung điểm của DI, \(NK\parallel IH\left( {BK\parallel IH} \right).\)

Do đó K là trung điểm của DH hay DK = KH (2)

Từ (1) và (2) \( \Rightarrow DK = KH = HC \Rightarrow {{DK} \over {DC}} = {1 \over 3}.\)