Bài 1. Phân tích đa thức \({x^6} – {x^4} + 2{x^3} + 2{x^2}\) thành nhân tử.
Bài 2. Rút gọn : \(A = {{ab – 4b – 2a + 8} \over {2a + 8 – ab – 4b}}:{{2a – 8 – ab + 4b} \over {ab + 4b – 2a – 8}}.\)
Bài 3. Cho biểu thức : \(P = \left( {{{{x^2} – 2x} \over {2{x^2} + 8}} – {{2{x^2}} \over {8 – 4x + 2{x^2} – {x^3}}}} \right).\left( {1 – {1 \over x} – {2 \over {{x^2}}}} \right)\) \(\left( {x \ne 0;x \ne 2} \right)\)
a) Rút gọn biểu thức P.
b) Tính giá trị của P với \(x \ne {1 \over 2}.\)
Bài 4. Tìm giá trị nguyên của x để giá trị của phân thức
\(Q = {{2{x^3} + {x^2} + 2x + 4} \over {2x + 1}}\) là số nguyên.
Bài 5. Cho tam giác ABC vuông tại A. Từ trung điểm I của cạnh BC, kẻ các đường thẳng song song với AB cắt AC tại N và song song với AC cắt AB tại M.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Dựng E là điểm đối xứng của I qua M, chứng minh NE đi qua trung điểm O của AM.
Bài 6. Cho hình vuông ABCD, trên cạnh DC lấy điểm E, từ A dựng đường thẳng vuông góc với AE tại A, đường này cắt đường thẳng BC tại F.
a) Chứng tỏ AF = AE.
b)Từ E dựng đường thẳng song song với đường thẳng AF và từ F dựng đường thẳng song song với đường thẳng AE, hai đường thẳng này cắt nhau tại G. Chứng tỏ AEGF là hình vuông.
c)Chứng tỏ ba đường thẳng BD, AG, EF đồng quy.
Advertisements (Quảng cáo)
Bài 1. \({x^6} – {x^4} + 2{x^3} + 2{x^2}\)
\(= {x^2}\left( {{x^4} – {x^2} + 2x + 2} \right) \)
\(= {x^2}\left[ {{x^2}\left( {{x^2} – 1} \right) + 2\left( {x + 1} \right)} \right]\)
\( = {x^2}\left( {x + 1} \right)\left( {{x^3} – {x^2} + 2} \right) \)
\(= {x^2}\left( {x + 1} \right)\left[ {\left( {{x^3} + 1} \right) – \left( {{x^2} – 1} \right)} \right]\)
\( = {x^2}\left( {x + 1} \right)\left( {x + 1} \right)\left( {{x^2} – x + 1 – x + 1} \right) \)
\(= {x^2}{\left( {x + 1} \right)^2}\left( {{x^2} – 2x + 2} \right).\)
Bài 2. Điều kiện: \(a \ne \pm 4;b \ne 2.\)
\(A = {{b\left( {a – 4} \right) – 2\left( {a – 4} \right)} \over {2\left( {a + 4} \right) – b\left( {a + 4} \right)}}:{{2\left( {a – 4} \right) – b\left( {a – 4} \right)} \over {b\left( {a + 4} \right) – 2\left( {a + 4} \right)}}\)
\(= {{\left( {a – 4} \right)\left( {b – 2} \right)} \over {\left( {a + 4} \right)\left( {2 – b} \right)}}:{{\left( {a – 4} \right)\left( {2 – b} \right)} \over {\left( {a + 4} \right)\left( {b – 2} \right)}}\)
Advertisements (Quảng cáo)
\( = {{\left( {a – 4} \right)\left( {b – 2} \right)} \over {\left( {a + 4} \right)\left( {2 – b} \right)}}.{{\left( {a + 4} \right)\left( {b – 2} \right)} \over {\left( {a – 4} \right)\left( {2 – b} \right)}} = {{{{\left( {b – 2} \right)}^2}} \over {{{\left( {2 – b} \right)}^2}}} = 1.\)
Bài 3. a) \(P = \left[ {{{{x^2} – 2x} \over {2\left( {{x^4} + 4} \right)}} – {{2{x^2}} \over {4\left( {2 – x} \right) + {x^2}\left( {2 – x} \right)}}} \right].{{{x^2} – x – 2} \over {{x^2}}}\)
\( = {{x{{\left( {x – 2} \right)}^2} + 4{x^2}} \over {2\left( {{x^2} + 4} \right)\left( {x – 2} \right)}}.{{{x^2} – x – 2} \over {{x^2}}} = {{x\left( {{x^2} + 4} \right)\left( {x + 1} \right)\left( {x – 2} \right)} \over {2{x^2}\left( {{x^2} + 4} \right)\left( {x – 2} \right)}} = {{x + 1} \over {2x}}.\)
b)Khi \(x = {1 \over 2} \Rightarrow P = {3 \over 2}.\)
Bài 4.\(Q = {x^2} + 1 + {3 \over {2x + 1}}\)
khi và và \(2x + 1 = \pm 1;2x + 1 = \pm 3\)
\( \Rightarrow x = 0; – 1;1; – 2.\)
Bài 5.
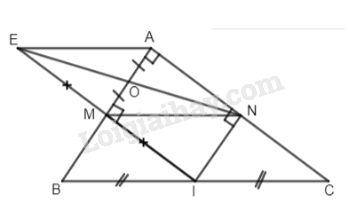
a) Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b)E đối xứng với I qua M nên EM = IM.
Lại có \(IM\parallel AN\) và \(IM = AN\left( {cmt} \right) \Rightarrow EM\parallel AN\) và \(EM = AN.\)
Do đó tứ giác ANME là hình bình hành mà O là trung điểm của AM nên đường chéo thứ hai EN phải qua O.
Bài 6.
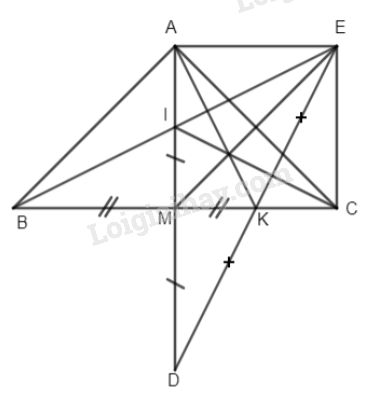
a) Ta có \(\widehat {{A_1}} = \widehat {{A_3}}\) (cùng phụ với \(\widehat {{A_2}}\) )
Xét hai tam giác vuông ABF và ADE có
\(\widehat {{A_1}} = \widehat {{A_3}}\left( {cmt} \right),AB = AD\left( {gt} \right)\)
Do đó \(\Delta ABF = \Delta ADE\left( {g.c.g} \right)\)
\( \Rightarrow AF = AE.\)
b) Ta có \(EG\parallel AF,AE\parallel FG\) nên tứ giác AEGF là hình bình hành có hai cạnh kề bằng nhau : \(AF = AE\) nên là hình vuông.
c) Gọi O là giao điểm của hai đường chéo AG và FE của hình vuông AEGF nên O là trung điểm của EF \) \Rightarrow \) Tam giác vuông FCE có OC là đường trung tuyến nên \(OC = {1 \over 2}EF.\)
Lại có \(OA = {1 \over 2}EF.\) Do đó OA = OC. Chứng tỏ O thuộc đường trung trực của đoạn AC hay O thuộc BD. (Hai đường chéo của hình vuông là đường trung trực của nhau).
Vậy BD, AG, EF đồng quy tại O.
