1. (2,5đ): Cho biểu thức \(P = \left( {\dfrac{1}{{x – 2}} – \dfrac{{{x^2}}}{{8 – {x^3}}}.\dfrac{{{x^2} + 2x + 4}}{{x + 2}}} \right):\dfrac{1}{{{x^2} – 4}}\)
a) Tìm điều kiện của x để P có nghĩa và rút gọn P.
b) Tìm giá trị nhỏ nhất của biểu thức P.
c) Tìm các số nguyên x để \(P \vdots \left( {{x^2} + 1} \right)\).
2. (2đ): Phân tích các đa thức sau thành nhân tử:
\(A\left( x \right) = 2{x^2} + x – 3\)
\(B\left( {a;b;c} \right) = \left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) + abc\)
3. (1đ): Cho hai đa thức \(P\left( x \right) = {x^3} + ax + b\)và \(Q\left( x \right) = {x^2} – 3x + 2\). Xác định các hệ số a, b sao cho với mọi giá trị của x thì \(P\left( x \right) \vdots Q\left( x \right)\).
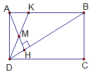
4. (3,5đ): Cho hình thoi ABCD có góc D bằng \({60^o}\). Gọi E, H, G, Flần lượt là trung điểm của AB, BC, CD và DA.
a) Chứng minh tứ giác EFGH là hình chữ nhật.
b) Cho AG cắt HF tại J. Chứng minh rằng \(HF = 4FJ\).
c) Gọi I là trung điểm của FJ và P là giao điểm của EH và DB. Chứng minh IG vuông góc với IP.
d) Cho \(AB = 2cm\). Tính độ dài IP.
5. (1đ): a) Cho ba số a, b, c thỏa mãn \(\left( {a + b + c} \right)\left( {ab + bc + ca} \right) = 2017\) và \(abc = 2017\).
Tính giá trị của biểu thức \(P = \left( {{b^2}c + 2017} \right)\left( {{c^2}a + 2017} \right)\left( {{a^2}b + 2017} \right)\).
b) (Dành riêng cho lớp 8A) Tìm các số tự nhiên x, n sao cho số \(p = {x^4} + {2^{4n + 2}}\) là một số nguyên tố.

1. Cho biểu thức \(P = \left( {\dfrac{1}{{x – 2}} – \dfrac{{{x^2}}}{{8 – {x^3}}}.\dfrac{{{x^2} + 2x + 4}}{{x + 2}}} \right):\dfrac{1}{{{x^2} – 4}}\)
a) Tìm điều kiện của x để P có nghĩa và rút gọn P.
ĐKXĐ: \(\left\{ \begin{array}{l}x – 2 \ne 0\\8 – {x^3} \ne 0\\x + 2 \ne 0\\{x^2} – 4 \ne 0\end{array} \right. \Leftrightarrow x \ne \pm 2\)
\(\begin{array}{l}P = \left( {\dfrac{1}{{x – 2}} – \dfrac{{{x^2}}}{{8 – {x^3}}}.\dfrac{{{x^2} + 2x + 4}}{{x + 2}}} \right):\dfrac{1}{{{x^2} – 4}}\\\;\;\; = \left( {\dfrac{1}{{x – 2}} + \dfrac{{{x^2}}}{{{x^3} – 8}}.\dfrac{{{x^2} + 2x + 4}}{{x + 2}}} \right):\dfrac{1}{{{x^2} – 4}}\\\;\;\; = \left( {\dfrac{1}{{x – 2}} + \dfrac{{{x^2}}}{{\left( {x – 2} \right)\left( {{x^2} + 2x + 4} \right)}}.\dfrac{{{x^2} + 2x + 4}}{{x + 2}}} \right):\dfrac{1}{{{x^2} – 4}}\\\;\;\; = \left( {\dfrac{1}{{x – 2}} + \dfrac{{{x^2}}}{{\left( {x – 2} \right)\left( {x + 2} \right)}}} \right).\left( {{x^2} – 4} \right)\\\;\;\; = \dfrac{{x + 2 + {x^2}}}{{{x^2} – 4}}.\left( {{x^2} – 4} \right) = {x^2} + x + 2.\end{array}\)
b) Tìm giá trị nhỏ nhất của biểu thức P.
\(P = {x^2} + x + 2 = \left( {{x^2} + x + \dfrac{1}{4}} \right) + \dfrac{7}{4} = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{7}{4} \ge \dfrac{7}{4}\)với mọi \(x \ne \pm 2\)
Dấu “=” xảy ra \( \Leftrightarrow x + \dfrac{1}{2} = 0 \Leftrightarrow x = – \dfrac{1}{2}\)
Vậy \({\min _P} = \dfrac{7}{4}\) đạt được khi \(x = – \dfrac{1}{2}\)
c) Tìm các số nguyên x để \(P \vdots \left( {{x^2} + 1} \right)\).
Để \(P \vdots \left( {{x^2} + 1} \right)\) thì phép chia trên phải có số dư là 0 \( \Rightarrow x + 1 = 0 \Leftrightarrow x = – 1\)
Vậy \(x = – 1.\)
2. Phân tích các đa thức sau thành nhân tử:
Advertisements (Quảng cáo)
\(A\left( x \right) = 2{x^2} + x – 3 = 2{x^2} + 3x – 2x – 3 = x\left( {2x + 3} \right) – \left( {2x + 3} \right) = \left( {2x + 3} \right)\left( {x – 1} \right)\)
\(\begin{array}{l}B\left( {a;b;c} \right) = \left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) + abc = \left( {ab + ac + {b^2} + bc} \right)\left( {c + a} \right) + abc\\ = abc + {a^2}b + a{c^2} + {a^2}c + {b^2}c + a{b^2} + b{c^2} + abc + abc\\ = \left( {{a^2}b + abc + {a^2}c} \right) + \left( {a{b^2} + {b^2}c + abc} \right) + \left( {abc + b{c^2} + a{c^2}} \right)\\ = a(ab + bc + ca) + b(ab + bc + ca) + c(ab + bc + ca)\\ = \left( {a + b + c} \right)(ab + bc + ca)\end{array}\)
3. Cho hai đa thức \(P\left( x \right) = {x^3} + ax + b\) và \(Q\left( x \right) = {x^2} – 3x + 2\). Xác định các hệ số a, b sao cho với mọi giá trị của x thì \(P\left( x \right) \vdots Q\left( x \right)\).
Để \(P\left( x \right) \vdots Q\left( x \right)\) với mọi giá trị của x\( \Leftrightarrow \left( {a + 7} \right)x + b – 6 = 0\)với mọi giá trị của x
\( \Leftrightarrow \left\{ \begin{array}{l}a + 7 = 0\\b – 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 7\\b = 6\end{array} \right.\)
Vậy với \(a = – 7\) và \(b = 6\) thì \(P\left( x \right) \vdots Q\left( x \right)\) với mọi giá trị của x.
4.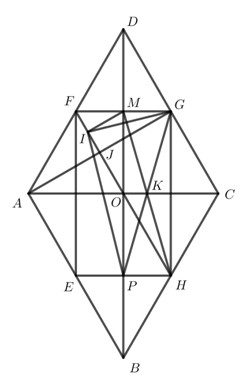
Cho hình thoi ABCD có góc D bằng \({60^o}\). Gọi E, H, G, F lần lượt là trung điểm của AB, BC, CD và DA.
a) Chứng minh tứ giác EFGH là hình chữ nhật.
Ta có ABCD là hình thoi \( \Rightarrow AC \bot BD\) (tính chất) (1)
Có E, F lần lượt là trung điểm của ABvà DA(gt)
\( \Rightarrow \) EF là đường trung bình trong tam giác ABD\( \Rightarrow \)EF // BD (2)
Có F, Glần lượt là trung điểm củaADvà CD(gt)
\( \Rightarrow \) FG là đường trung bình trong tam giác DAC\( \Rightarrow \)FG // AC (3)
Từ (1), (2), (3) \( \Rightarrow EF \bot FG\) (từ vuông góc đến song song)
Tương tự \( \Rightarrow FG \bot GH\,\,;\,\,GH \bot HE\,\,;\,\,HE \bot EF\)
\( \Rightarrow \)EFGH là hình chữ nhật (dhnb)
b) Cho AG cắt HF tại J. Chứng minh rằng \(HF = 4FJ\).
Ta có F, Hlần lượt là trung điểm của ADvà BC
Advertisements (Quảng cáo)
\( \Rightarrow \) FHlà đường trung bình của hình thoi ABCD\( \Rightarrow \)FH // AB // CD và \(FH = AB = CD\)
Xét tam giác ADG có F là trung điểm của AD, FJ // DG (FH // CD)
\( \Rightarrow \)J là trung điểm của AG \( \Rightarrow \)FJ là đường trung bình trong tam giác ADG
\( \Rightarrow FJ = \dfrac{1}{2}DG = \dfrac{1}{4}CD = \dfrac{1}{4}HF\)(do G là trung điểm của CD nên \(DG = \dfrac{1}{2}CD\))
\( \Rightarrow HF = 4FJ\) (đpcm)
c) Gọi I là trung điểm của FJ và P là giao điểm của EH và DH. Chứng minh IG vuông góc với IP.
Gọi AC cắt BD tại O\( \Rightarrow DO = \dfrac{1}{2}BD\,\,;\,\,OC = OA = \dfrac{1}{2}AC\) (tính chất)
Xét tam giác ACD có \(DA = DC\) (ABCD là hình thoi), \(\angle D = {60^o}\) (gt)
\( \Rightarrow \)\(\Delta ACD\) đều (dhnb) \( \Rightarrow AC = CD\,\)\(;\,\,DO = AG\)(tính chất)
\( \Rightarrow AG\) vừa là trung tuyến vừa là đường cao \( \Rightarrow AG \bot CD \Rightarrow AG \bot HF\) (từ vuông góc đến song song)
Gọi FG cắt BD tại M
Xét tam giác ODA có Flà trung điểm của AD, FM // OA (FG // AC)
\( \Rightarrow \)Mlà trung điểm của OD\( \Rightarrow \)FM là đường trung bình trong tam giác ODA\( \Rightarrow FM = \dfrac{1}{2}OA\)
Tương tự ta cũng được \(GM = \dfrac{1}{2}OC\) mà \(OA = OC\) (cmt) \( \Rightarrow FM = GM\)
\( \Rightarrow \)M là trung điểm của FG
\( \Rightarrow \) IM là đường trung bình trong tam giác FJG
\( \Rightarrow \)IM // AG mà \(AG \bot HF\) (cmt)\( \Rightarrow IM \bot HF\)
Gọi PG cắt MH tại K.
Dễ thấy PHGM là hình chữ nhật (có 3 góc vuông)
\( \Rightarrow \)K là trung điểm của PG và HM ; \(HM = PG\)
Có tam giác IMH vuông tại I (\(IM \bot HF\)) có K là trung điểm của HM
\( \Rightarrow \)\(KI = \dfrac{1}{2}HM = \dfrac{1}{2}PG\)
\( \Rightarrow \) Tam giác PIG vuông tại I\( \Rightarrow \)\(IG \bot IP\) (đpcm)
d) Cho \(AB = 2cm\). Tính độ dài IP.
Ta có ABCD là hình thoi có HF là đường trung bình và\(\Delta ACD\) đều
\( \Rightarrow AB = BC = CD = DA = AC = HF = 2cm\)
\( \Rightarrow AG = \dfrac{{2\sqrt 3 }}{2} = \sqrt 3 cm \Rightarrow GJ = \dfrac{1}{2}AG = \dfrac{{\sqrt 3 }}{2}cm\) (J là trung điểm của AG)
\(OC = OA = \dfrac{1}{2}AC = 1cm\) ; \(FG = EH = \dfrac{1}{2}AC = 1cm\)
\(OD = AG = \sqrt 3 cm \Rightarrow EF = GH = OD = \dfrac{1}{2}BD = \sqrt 3 cm\)
\(IJ = \dfrac{1}{2}FJ = \dfrac{1}{8}HF = \dfrac{1}{4}cm\) ; \(PH = MG = \dfrac{1}{2}FG = \dfrac{1}{2}cm\)
Áp dụng định lý Pytago cho tam giác GJI vuông tại Jta được:
\(IG = \sqrt {I{J^2} + G{J^2}} = \sqrt {\dfrac{1}{{16}} + \dfrac{3}{4}} = \dfrac{{\sqrt {13} }}{4}\left( {cm} \right)\)
Áp dụng định lý Pytago cho tam giác HPG vuông tại H ta được:
\(PG = \sqrt {P{H^2} + G{H^2}} = \sqrt {\dfrac{1}{4} + 3} = \dfrac{{\sqrt {13} }}{2}\left( {cm} \right)\)
Áp dụng định lý Pytago cho tam giác PIG vuông tại I ta được:
\(IP = \sqrt {P{G^2} – I{G^2}} = \sqrt {\dfrac{{13}}{4} – \dfrac{{13}}{{16}}} = \dfrac{{\sqrt {39} }}{4}\left( {cm} \right)\)
5. a) Cho ba số a, b, c thỏa mãn \(\left( {a + b + c} \right)\left( {ab + bc + ca} \right) = 2017\) và \(abc = 2017\).
Tính giá trị của biểu thức \(P = \left( {{b^2}c + 2017} \right)\left( {{c^2}a + 2017} \right)\left( {{a^2}b + 2017} \right)\).
Theo câu 2 ta có \(\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) + abc = \left( {a + b + c} \right)(ab + bc + ca)\)
\(\begin{array}{l} \Rightarrow \left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) = \left( {a + b + c} \right)(ab + bc + ca) – abc = 2017 – 2017 = 0\\P = \left( {{b^2}c + 2017} \right)\left( {{c^2}a + 2017} \right)\left( {{a^2}b + 2017} \right)\\\;\;\; = \left( {{b^2}c + abc} \right)\left( {{c^2}a + abc} \right)\left( {{a^2}b + abc} \right)\\\;\;\; = bc\left( {c + a} \right)ca\left( {c + b} \right)ab\left( {a + c} \right)\\\;\;\; = {a^2}{b^2}{c^2}\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) = 0.\end{array}\)
b) (Dành riêng cho lớp 8A) Tìm các số tự nhiên x, n sao cho số \(p = {x^4} + {2^{4n + 2}}\) là một số nguyên tố.
\(\begin{array}{l}p = {x^4} + {2^{4n + 2}} = {\left( {{x^2}} \right)^2} + 2.{x^2}{.2^{2n + 1}} + {\left( {{2^{2n + 1}}} \right)^2} – 2.{x^2}{.2^{2n + 1}}\\\;\;\; = {\left( {{x^2} + {2^{2n + 1}}} \right)^2} – {x^2}{.2^{2n + 2}}\\\;\;\; = \left( {{x^2} + {2^{2n + 1}} – x{{.2}^{n + 1}}} \right)\left( {{x^2} + {2^{2n + 1}} + x{{.2}^{n + 1}}} \right).\end{array}\)
Với mọi số tự nhiên x, n\( \Rightarrow {2^{2n + 1}} \ge {2^1} = 2 \Rightarrow {x^2} + {2^{2n + 1}} + x{.2^{n + 1}} \ge 2\)
Với mọi số tự nhiên x, n \( \Rightarrow {2^{2n}}\) \( \ge 1 \Rightarrow {x^2} + {2^{2n + 1}} – x{.2^{n + 1}} = {x^2} – 2x{.2^n} + {2^{2n}} + {2^{2n}} = {\left( {x – {2^n}} \right)^2} + {2^{2n}} \ge 1\)
Để p là một số nguyên tố \(\left\{ \begin{array}{l}{x^2} + {2^{2n + 1}} – x{.2^{n + 1}} = 1\\{x^2} + {2^{2n + 1}} + x{.2^{n + 1}} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{2^{2n + 1}} = 2\\x – {2^n} = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2n + 1 = 1\\x = {2^n}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n = 0\\x = {2^0} = 1\end{array} \right..\)
Vậy với \(n = 0\)và \(x = 1\) thỏa mãn yêu cầu đề bài.