PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2đ)
Lựa chọn chữ cái đứng trước câu trả lời đúng
1. : Kết quả của phép tính \(8{x^2}:4x\) là:
A.\(2\) B.\( – 2x\)
C.\(2x\) D.\( – 2\)
2. : Biểu thức \({x^2} – {y^2}\) bằng:
A.\((x + y)(x + y)\)
B.\((x – y)(x + y)\)
C.\({x^2} + 2xy + {y^2}\)
D.\({x^2} – 2xy + {y^2}\)
3. : Phân tích đa thức \(x{y^2} + 2xy + x\) ta được:
A.\(x(x + 1)\) B.\(x{(y + 1)^2}\)
C.\((x – 1)(x + y)\) D.\(y{(x + 1)^2}\)
4. : Tổng của hai phân thức \(\dfrac{3}{{7xy}} + \dfrac{4}{{7xy}}\) là
A.\(\dfrac{1}{{xy}}\) B.\(\dfrac{3}{{xy}}\)
C.\(\dfrac{4}{{xy}}\) D.\(\dfrac{7}{{xy}}\)
5. : Hình nào sau đây không có tâm đối xứng?
A.Hình bình hành
B.Hình chữ nhật
C.Hình thang cân
D.Cả ba hình trên
6. : Hình thang cân là:
A.Hình thang có hai góc kề một đáy bằng nhau.
B.Tứ giác có các cạnh đối song song
Advertisements (Quảng cáo)
C.Hình thang có hai cạnh bên bằng nhau
D.Hình thang có hai đường chéo bằng nhau
7. : Cho tam giác vuông như hình vẽ:
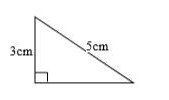
Diện tích của tam giác bằng:
A.\(7c{m^2}\) B.\(6c{m^2}\)
C.\(8c{m^2}\) D.\(4c{m^2}\)
PHẦN II. TỰ LUẬN (8đ)
8. (2đ):Thực hiện phép tính:
\(a)\,\,2x.(3{x^2} + 1)\\b)\,\,\left( {2{x^3} – 5{x^2} + 6x} \right):2x\)
9. (1đ):
a) Tìm \(x\) biết: \({x^2} + 5x = 0\) .
b) Phân tích đa thức sau thành nhân tử: \({x^2} – 2x – xy + 2y\).
1.0 (2đ):Cho \(Q = \dfrac{{2(x – 2)}}{{6(x – 2)}}\)
a) Tìm điều kiện xác định của \(Q\).
Advertisements (Quảng cáo)
b) Thu gọn biểu thức \(Q\).
1.1 (2đ):Một mảnh vườn lúc đầu có dạng tam giác \(ABC\) vuông tại \(A\), bờ rào \(AB\) dài \(5m\), rào \(AC\) dài \(12m\). Người ta sử dụng lưới ngăn dọc theo hai điểm \(E,\,\,M\)(\(E\) là trung điểm của \(AC\) và \(M\) là trung điểm của \(BC\)) để chia mảnh vườn thành hai phần trồng rau và hoa.
a) Tính độ dài của lưới \(ME\) phải dùng.
b) Mảnh vườn \(AEMB\) là hình gì? Vì sao?
c) Tính diện tích mảnh vườn \(AEMB\).
1.2 (1đ): a) Tìm giá trị nhỏ nhất của \(A = {x^2} – 2x + 3\) với mọi số thực \(x \in Z\).
b) Tìm giá trị nguyên của \(n\) để \(({n^3} – 3{n^2} + n)\,\, \vdots \,\,(n – 3)\).
I. Trắc nghiệm
|
1. C |
2. B |
3. B |
4. A |
|
5. C |
6. A; D |
7. B |
|
II. TỰ LUẬN: (7đ)
8. Ta có:
\(\begin{array}{l}a)\,\,2x.(3{x^2} + 1) = 2x.3{x^2} + 2x.1 = 6{x^3} + 2x\\b)\,\,\left( {2{x^3} – 5{x^2} + 6x} \right):2x \\= 2{x^3}:2x – 5{x^2}:2x + 6x:2x\\ = {x^2} – \dfrac{5}{2}x + 3\end{array}\)
9. a) \({x^2} + 5x = 0 \Rightarrow x(x + 5) = 0 \)
\(\Rightarrow \left[ \begin{array}{l}x = 0\\x + 5 = 0\end{array} \right.\)
\(\Rightarrow \left[ \begin{array}{l}x = 0\\x = – 5\end{array} \right.\)
Vậy nghiệm của phương trình đã cho là \(x = 0\) hoặc \(x = – 5\)
b) Ta có:
\({x^2} – 2x – xy + 2y \)
\(= ({x^2} – 2x) – (xy – 2y) \)
\(= x(x – 2) – y(x – 2) = (x – 2)(x – y)\).
10: a) ĐKXĐ: \(6(x – 2) \ne 0\,\,\,\, \Rightarrow x – 2 \ne 0\,\,\,\, \Rightarrow x \ne 2\)
b) Với \(x \ne 2\) thì ta có: \(Q = \dfrac{{2(x – 2)}}{{6(x – 2)}} = \dfrac{2}{6} = \dfrac{1}{3}\)
11
|
|
a) Theo giả thiết ta có \(M\) và \(E\) lần lượt là trung điểm của \(BC\) và \(AC\) nên \(ME\) là đường trung bình của \(\Delta ABC\) (khái niệm)
\( \Rightarrow ME\) // \(AB\) \(\,\,;\,\,\,ME = \dfrac{1}{2}AB = \dfrac{1}{2}.5 = 2,5m\).(tính chất)
b) Vì \(ME\) // \(AB;\,\,AB \bot AE\) nên tứ giác \(AEMB\) là hình thang vuông.
Vậy mảnh vườn \(AEMB\) là hình thang vuông.
c) Diện tích phần vườn \(AEMB\) là:
\({S_{AEMB}} = \dfrac{{(ME + AB).AE}}{2} = \dfrac{{(2,5 + 5).6}}{2} = 22,5\,\,({m^2})\)
12: a) Ta có: \({x^2} – 2x + 3 = {x^2} – 2x + 1 + 2 = {(x – 1)^2} + 2\)
Ta thấy \({(x – 1)^2} \ge 0\) với mọi \(x\), do đó \({(x – 1)^2} + 2 \ge 2\) với mọi \(x\).
Vậy \(A = {x^2} – 2x + 3\) đạt giá trị nhỏ nhất là \(2\).
Đẳng thức xảy ra khi \(x – 1 = 0\), hay \(x = 1\).
b) Ta có: \(({n^3} – 3{n^2} + n):(n – 3) = {n^2} – 1 + \dfrac{3}{{n – 3}}\) .
Điều kiện \(n \ne 3.\)
Do đó để \(({n^3} – 3{n^2} + n)\,\, \vdots \,\,(n – 3)\)thì \(n – 3\) phải là ước của \(3\), hay \(n – 3 \in {\rm{\{ }} – 3\,;\,\, – 1\,;\,\,1\,;\,\,3{\rm{\} }}\).
Ta có bảng sau:
|
\(n – 3\) |
\( – 3\) |
\( – 1\) |
\(1\) |
\(3\) |
|
\(n\) |
\(0\)(tm) |
\(2\)(tm) |
\(4\)(tm) |
\(6\) ™ |
Vậy để \(({n^3} – 3{n^2} + n)\,\, \vdots \,\,(n – 3)\)thì \(n \in {\rm{\{ 0; 2; 4; 6\} }}\).
