A. TRẮC NGHIỆM (2,0đ)
1. : (1,0đ) Chọn phương án trả lời đúng cho các câu sau:
1. Kết quả rút gọn của \(\dfrac{{ – 4{x^2} – 4x}}{{1 – {x^2}}}\)là:
A. \(\dfrac{{ – 4x}}{{1 + x}}\) B. \(\dfrac{{ – 4x}}{{x – 1}}\)
C. \(\dfrac{{4x}}{{x – 1}}\) D. \(\dfrac{{4x}}{{x + 1}}\)
2. Thực hiện phép chia \({x^3} + 27\) cho \(3x – {x^2} – 9\) ta được thương là:
A. \(x + 3\) B. \( – x – 3\)
C. \(x – 3\) D. \( – x + 3\)
2. : (1,0đ) Trong các câu sau, câu nào đúng, câu nào sai:
a) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường là hình thoi.
b)Tứ giác có một cặp cạnh đối song song và cặp cạnh đối còn lại bằng nhau là hình thang cân.
c) Hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau.
d) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
B. TỰ LUẬN (8,0đ)
1. (1,5đ):Phân tích các đa thức sau thành nhân tử:
a) \({x^2} – 9x – 9y – {y^2}\)
b) \(2xy – {x^2} – {y^2} + 16\)
c) \({x^3} – {x^2} – 6x\)
2. (2,5đ):Cho biểu thức:\(A = \left( {\dfrac{{3{x^2}}}{{{x^2} – 4}} – \dfrac{3}{{x + 2}} + \dfrac{3}{{2 – x}}} \right):\dfrac{{x + 3}}{{x + 2}}\)
a) Rút gọn biểu thức A.
b) Tính giá trị biểu thức A khi \(\left| {x – 2} \right| = 4\).
c) Tìm giá trị nguyên của x để biểu thức A có giá trị là một số nguyên.
3. (3,5đ):Cho hình chữ nhật ABCD. Kẻ AN và CM cùng vuông góc với BD (\(M,\,\,N \in BD\))
a) Chứng minh tứ giác ANCM là hình bình hành.
b)Gọi K là điểm đối xứng với điểm A qua N. Chứng minh MNKC là hình chữ nhật.
c) Tứ giác DKCB là hình gì? Tại sao?
d) Tia AM cắt tia KC tại P. Chứng minh các đường thẳng PN, AC, KM đồng quy.
4. (0,5đ):Cho x, y là hai số thực khác 0 thỏa mãn: \(2{x^2} + \dfrac{{{y^2}}}{4} + \dfrac{1}{{{x^2}}} = 4\).
Tìm giá trị lớn nhất và giá trị nhỏ nhất của \(A = 2016 + xy\)
I. TRẮC NGHIỆM
1. 1.Chọn C.
2. Chọn B.
2. a) Vì tứ giác cắt nhau tại trung điểm của mỗi đường là hình thoi đúng theo dấu hiệu nhận biết của hình thoi nên a) đúng.
b) Tứ giác có 1 cặp cạnh đối song song với nhau thì tứ giác đó là hình thang. Hình thang có hai cạnh bên bằng nhau có thể là hình bình hành nên b) sai.
Advertisements (Quảng cáo)
c) Hai tam giác có diện tích bằng nhau nhưng hai tam giác đó có thể không bằng nhau nên c) sai.
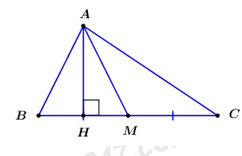
Khi đó:
\({S_{AMB}} = \dfrac{1}{2}AH.BM;\;\;\;{S_{AMC}} = \dfrac{1}{2}AH.MC\)
Mà \(MB = MC \Rightarrow {S_{ABM}} = {S_{AMC}}.\)
Nhưng \(\Delta ABM\) và \(\Delta ACM\) không bằng nhau.
d) Tứ giác có 2 cạnh đối song song và bằng nhau thì tứ giác đó là hình bình hành theo dấu hiện nhận biết của hình bình hành nên d) đúng.
II. TỰ LUẬN
1. Phân tích các đa thức sau thành nhân tử:
a) \({x^2} – 9x – 9y – {y^2} \)
\(= \left( {{x^2} – {y^2}} \right) – \left( {9x + 9y} \right) \)
\(= \left( {x – y} \right)\left( {x + y} \right) – 9\left( {x + y} \right) \)
\(= \left( {x + y} \right)\left( {x – y – 9} \right)\)
b) \(2xy – {x^2} – {y^2} + 16 \)
\(= 16 – \left( {{x^2} – 2xy + {y^2}} \right) \)
\(= 16 – {\left( {x – y} \right)^2} \)
\(= \left( {4 – x + y} \right)\left( {4 + x – y} \right)\)
\(\begin{array}{l}c)\;{x^3} – {x^2} – 6x = x\left( {{x^2} – x – 6} \right) \\= x\left( {{x^2} – 3x + 2x – 6} \right)\\ = x\left[ {x\left( {x – 3} \right) + 2\left( {x – 3} \right)} \right]\\ = x\left( {x – 3} \right)\left( {x + 2} \right).\end{array}\)
2. Cho biểu thức: \(A = \left( {\dfrac{{3{x^2}}}{{{x^2} – 4}} – \dfrac{3}{{x + 2}} + \dfrac{3}{{2 – x}}} \right):\dfrac{{x + 3}}{{x + 2}}\)
a) Rút gọn biểu thức A.
Điều kiện xác định \(x \ne \pm 2\)
\(\begin{array}{l}A = \left( {\dfrac{{3{x^2}}}{{{x^2} – 4}} – \dfrac{3}{{x + 2}} + \dfrac{3}{{2 – x}}} \right):\dfrac{{x + 3}}{{x + 2}}\\ = \dfrac{{3{x^2} – 3.\left( {x – 2} \right) – 3\left( {x + 2} \right)}}{{\left( {x – 2} \right)\left( {x + 2} \right)}}.\dfrac{{x + 2}}{{x + 3}}\\ = \dfrac{{3{x^2} – 3x + 6 – 3x – 6}}{{x – 2}}.\dfrac{1}{{x + 3}}\\ = \dfrac{{3{x^2} – 6x}}{{x – 2}}.\dfrac{1}{{x + 3}} = \dfrac{{3x\left( {x – 2} \right)}}{{x – 2}}.\dfrac{1}{{x + 3}} = \dfrac{{3x}}{{x + 3}}\end{array}\)
Advertisements (Quảng cáo)
b) Tính giá trị biểu thức A khi \(\left| {x – 2} \right| = 4\).
\(\left| {x – 2} \right| = 4 \Leftrightarrow \left[ \begin{array}{l}x – 2 = 4\\x – 2 = – 4\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}x = 6\,\,\,\,\,\,\,(tm)\\x = – 2\,\,\,\,(ktm)\end{array} \right.\)
Với \(x = 6\) thì \(A = \dfrac{{3.6}}{{6 + 3}} = \dfrac{{18}}{9} = 2\)
c) Tìm giá trị nguyên của x để biểu thức A có giá trị là một số nguyên.
\(A = \dfrac{{3x}}{{x + 3}} = \dfrac{{3\left( {x + 3} \right) – 9}}{{x + 3}} = 3 – \dfrac{9}{{x + 3}}\)
Đểbiểu thức A có giá trị là một số nguyên\( \Leftrightarrow \dfrac{9}{{x + 3}}\) nguyên\( \Leftrightarrow x + 3 \in \)Ư(9)
\( \Leftrightarrow x + 3 \in \left\{ {1; – 1;3; – 3;9; – 9} \right\}\) kết hợp điều kiện xác định
Ta có bảng giá trị:
|
\(x + 3\) |
\( – 9\) |
\( – 3\) |
\( – 1\) |
\(1\) |
\(3\) |
\(9\) |
|
\(x\) |
\( – 12\) |
\(0\) |
\( – 4\) |
\( – 2\) |
\( – 6\) |
\(6\) |
Kết hợp với điều kiện ta được \(x \in \left\{ { – 12;\; – 6;\; – 4;\;0;\;6} \right\}\) thỏa mãn.
Vậy với \(x \in \left\{ { – 12; – 6; – 4;0;6} \right\}\)thì biểu thức A có giá trị là một số nguyên.
3.
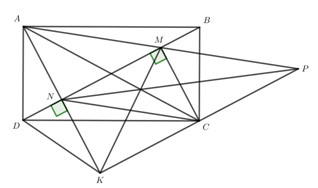
Cho hình chữ nhật ABCD. Kẻ AN và CM cùng vuông góc với BD\(\left( {M,\,\,N \in BD} \right)\)
a) Chứng minh tứ giác ANCM là hình bình hành.
Xét \(\Delta ADN\) và \(\Delta CBM\)có:
\(\angle AND = \angle CMB = {90^o}\) (AN và CM cùng vuông góc với BD);
\(AD = BC\) (ABCD là hcn)
\(\angle ADN = \angle CBM\) (hai góc so le trong)
\( \Rightarrow \Delta ADN = \Delta CBM\;\left( {ch – gn} \right) \Rightarrow AN = CM\)(2 cạnh tương ứng)
Mặt khác AN // CM (cùng vuông góc với BD) \( \Rightarrow ANCM\) là hình bình hành
b)Gọi K là điểm đối xứng với điểm A qua N. Chứng minh MNKC là hình chữ nhật.
Có K là điểm đối xứng với điểm A qua N\( \Rightarrow AN = NK\)mà \(AN = CM\) (cmt) \( \Rightarrow NK = CM\)
Kết hợp NK // CM (cùng vuông góc với BD) \( \Rightarrow \)MNKC là hình bình hành (dhnb)
Mà \(\angle CMN = {90^o}\;\left( {CM \bot BD} \right) \Rightarrow MNKC\) là hình chữ nhật (dhnb).
c) Tứ giác DKCB là hình gì? Tại sao?
Ta có: KC // MN (MNKC là hình chữ nhật) \( \Rightarrow KC//BD.\)
\( \Rightarrow DKCB\)là hình thang.
Có K là điểm đối xứng với điểm A qua N\( \Rightarrow \) N là trung điểm của AK(tính chất).
Mà \(DN \bot AK\;\;\left( {gt} \right) \Rightarrow DN\)là đường trung trực của \(AK \Rightarrow DA = DK\)(tính chất)
Lại có \(DA = BC\) (ABCD là hcn) \( \Rightarrow DK = BC\)
Vậy DKCB là hình thang cân (dhnb)
d) Tia AM cắt tia KC tại P. Chứng minh các đường thẳng PN, AC, KM đồng quy.
Ta có N là trung điểm của AK (cmt)\( \Rightarrow \)PN là trung tuyến ứng với cạnh AK trong \(\Delta AKP\) (1)
Ta có MN // KC (MNKC là hình chữ nhật) \( \Rightarrow \)MN // KP
Mà N là trung điểm của AK (cmt)\( \Rightarrow \)M là trung điểm của AP
\( \Rightarrow \)KM là trung tuyến ứng với cạnh AP trong \(\Delta AKP\)(2)
Mặt khácNC // AM(ANCM là hình bình hành) \( \Rightarrow \) NC // AP
Mà N là trung điểm của AK (cmt) \( \Rightarrow \)C là trung điểm của KP
\( \Rightarrow \)AC là trung tuyến ứng với cạnh KP trong \(\Delta AKP\)(3)
Từ (1), (2) và (3) \( \Rightarrow \)các đường thẳng PN, AC, KM đồng quy (là 3 đường trung tuyến trong \(\Delta AKP\))
4. Cho x, y là hai số thực khác 0 thỏa mãn: \(2{x^2} + \dfrac{{{y^2}}}{4} + \dfrac{1}{{{x^2}}} = 4\).
Tìm giá trị lớn nhất và giá trị nhỏ nhất của \(A = 2016 + xy\)
Ta có \(2{x^2} + \dfrac{{{y^2}}}{4} + \dfrac{1}{{{x^2}}} = 4\)
\(\Leftrightarrow \left( {{x^2} – 2 + \dfrac{1}{{{x^2}}}} \right) + \left( {{x^2} + xy + \dfrac{{{y^2}}}{4}} \right) = 2 + xy\)
\( \Leftrightarrow {\left( {x – \dfrac{1}{x}} \right)^2} + {\left( {x + \dfrac{y}{2}} \right)^2} = 2 + xy\)
\(VT \ge 0 \Rightarrow xy \ge – 2\).
Dấu bằng xảy ra \( \Leftrightarrow x = \dfrac{1}{x} = \dfrac{{ – y}}{2} \Leftrightarrow \left\{ \begin{array}{l}{x^2} = 1\\y = – 2x\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = – 2\end{array} \right.\\\left\{ \begin{array}{l}x = – 1\\y = 2\end{array} \right.\end{array} \right..\)
Vậy \({\min _A} = 2016 – 2 = 2014\) đạt được khi \(\left\{ \begin{array}{l}x = 1\\y = – 2\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}x = – 1\\y = 2\end{array} \right..\)
Ta có \(2{x^2} + \dfrac{{{y^2}}}{4} + \dfrac{1}{{{x^2}}} = 4\)
\(\Leftrightarrow \left( {{x^2} – 2 + \dfrac{1}{{{x^2}}}} \right) + \left( {{x^2} – xy + \dfrac{{{y^2}}}{4}} \right) = 2 – xy\)
\( \Leftrightarrow {\left( {x – \dfrac{1}{x}} \right)^2} + {\left( {x – \dfrac{y}{2}} \right)^2} = 2 – xy\)
\(VT \ge 0 \Rightarrow xy \le 2\).
Dấu bằng xảy ra \( \Leftrightarrow x = \dfrac{1}{x} = \dfrac{y}{2}\)
\(\Leftrightarrow \left\{ \begin{array}{l}{x^2} = 1\\y = 2x\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\\\left\{ \begin{array}{l}x = – 1\\y = – 2\end{array} \right.\end{array} \right..\)
Vậy \({\max _A} = 2016 + 2 = 2018\) đạt được khi \(\left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}x = – 1\\y = – 2\end{array} \right.\)
