
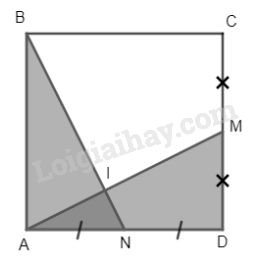
Bài 1. Cho hình vuông ABCD, M là trung điểm của CD, N là trung điểm của AD. Gọi I là giao điểm của AM và BN.
Chứng minh rằng: \({S_{DMIN}} = {S_{AIB}}.\)
Bài 2. Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB.
Chứng minh rằng: \({S_{ABCD}} = 2{S_{EDC}}.\)

Bài 1.
Advertisements (Quảng cáo)
Ta có: \(\Delta BAN = \Delta ADM\left( {c.g.c} \right)\)
\( \Rightarrow {S_{BAN}} = {S_{ADM}}\)
\( \Rightarrow {S_{BAN}} – {S_{AIN}} = {S_{ADM}} – {S_{AIN}}\)
Hay \({S_{AIB}} = {S_{DMIN}}.\)
Advertisements (Quảng cáo)
Bài 2.
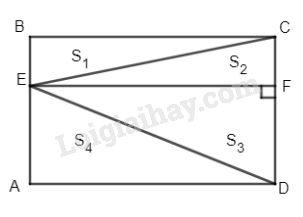
Kẻ \(EF \bot CD\) ta có: \(\Delta BCE = \Delta FEC\left( {c.g.c} \right)\) , tương tự \(\Delta AED = \Delta FDE.\)
Do đó (theo hình vẽ):
\({S_1} = {S_2}\) và \({S_3} = {S_4}\)
\( \Rightarrow {S_1} + {S_3} = {S_1} + {S_4} = {1 \over 2}{S_{ABCD}}\)
Hay \({S_{ECD}} = {1 \over 2}{S_{ABCD}} \Rightarrow {S_{ABCD}} = 2{S_{ECD}}.\)




![[THCS Phú Hòa Đông] thi học kì 2 môn Hóa lớp 8 năm 2020: Cho 16,8g sắt tác dụng với dung dịch axit HCl vừa đủ. Khi hiđro sinh ra được dẫn qua bột CuO nung nóng. Viết các phương trình hóa học của phản ứng xảy ra](https://dethikiemtra.com/wp-content/uploads/2020/09/bo-suu-tap-tranh-ve-co-giao-va-hoc-sinh-1-100x75.jpg)

