
Bài 1. Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD, I là trung điểm của cạnh AB, J là trung điểm của DC.
a) Chứng tỏ AJ = CI.
b) Chứng tỏ O là trung điểm của đoạn IJ.
Bài 2. Cho hình thoi ABCD có hai dường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC tại I và BC ở F.
a) Chứng minh ID = 2IF.
b) Nối EO cắt BC ở G, đường thẳng OF cắt EC ở H. Chứng minh ba điểm A, G, H thẳng hàng.
c) Biết \(\widehat {BAD} = {60^ \circ },AB = a.\) Tính diện tích hình thoi ABCD theo a.

Bài 1.
Advertisements (Quảng cáo)

a) I, J lần lượt là trung điểm của AB và CD
\( \Rightarrow AI\parallel CJ\) và AI = CJ.
Do đó tứ giác AICJ là hình bình hành
\( \Rightarrow {\rm{AJ}} = CI.\)
b) O là giao điểm hai đường chéo AC và BD nên O là trung điểm của AC. AICJ là hình bình hành (cmt). Do đó đường chéo thứ hai IJ phải qua O hay O là trung điểm của IJ.
Advertisements (Quảng cáo)
Bài 2.
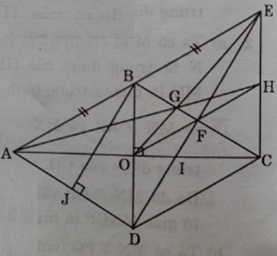
a) Ta có BE = BA (gt) mà \(BA\parallel CD\) và BA = CD (gt)
\( \Rightarrow BE\parallel CD\) và \(BE = CD.\)
Do đó BECD là hình bình hành nên F là trung điểm của BC.
Xét \(\Delta BDC\) có I là trọng tâm \( \Rightarrow ID = 2IF.\)
b) Ta có OF là đường trung bình của \(\Delta BDC \Rightarrow OF\parallel DC\)
Mà \(DC\parallel AB\) nên \(OF\parallel AE.\)
Vì O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của \(\Delta AEC\). Mà AH cắt EO tại G nên G là trọng tâm \(\Delta AEC \Rightarrow A,G,H\) thẳng hàng.
c) \(\Delta ABD\) cân (AB = AD (gt) có\(\widehat {BAD} = {60^ \circ }\) nên \(\Delta ABD\) đều.
Kẻ \(BJ \bot AD\) ta có: \(JA = JD = {{AD} \over 2} = {a \over 2}\)
\( \Rightarrow BJ = \sqrt {A{B^2} – A{J^2}} \)\(\;= \sqrt {{a^2} – {{\left( {{a \over 2}} \right)}^2}} = \sqrt {{{3{a^2}} \over 4}} = {{a\sqrt 3 } \over 2}.\)
Vậy \({S_{ABCD}} = AD.BJ = a.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 2}.\)

![[THCS Trần Cao] thi môn Toán lớp 8 cuối học kì 2: Mẫu số của một phân số lớn hơn tử số của nó là 5, nếu tăng cả tử lẫn mẫu của nó thêm 5 đơn vị thì được phân số mới bằng phân số 2 /3. Tìm phân số ban đầu](https://dethikiemtra.com/wp-content/uploads/2020/09/anh-chup-dep-ve-gia-dinh_035107328-100x75.jpg)




