
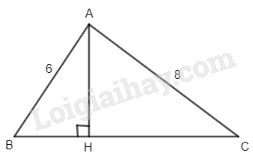
Bài 1. Tính đường cao của tam giác vuông biết hai cạnh góc vuông là 6 cm và 8 cm.
Bài 2. Cho tứ giác ABCD. Gọi M là trung điểm của AB, N là trung điểm của CD.
Chứng minh rằng: \({S_{MBN{\rm{D}}}} = {1 \over 2}{S_{ABCD}}.\)
Bài 3. Cho hình bình hành ABCD có I, J lần lượt là trung điểm của AB và CD.
a) Chứng minh AICJ là hình bình hành.
b) Biết diện tích hình bình hành ABCD bằng \(48c{m^2}\) . Tính diện tích AICJ.
c) Gọi E, F lần lượt là giao điểm của AJ, CJ với BD.
Chứng minh rằng BD = 3DE.

Bài 1
Advertisements (Quảng cáo)
Ta có: \(B{C^2} = A{B^2} + A{C^2}\)
\( = {6^2} + {8^2}\) (định lý Py – ta – go)
\( \Rightarrow BC = \sqrt {36 + 64} = \sqrt {100} = 10\left( {cm} \right)\)
\({S_{ABC}} = {1 \over 2}BC.AH = {1 \over 2}AB.AC\)
\( \Rightarrow BC.AH = AB.AC\)
\(\Rightarrow AH = \dfrac{AB.AC}{10} = 6,8\left( {cm} \right)\)
Advertisements (Quảng cáo)
Bài 2
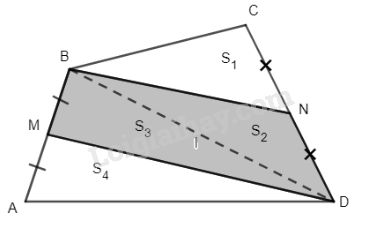
Nối đường chéo BD, \(\Delta BCD\) có BN là trung tuyến nên \({S_1} = {S_2}\) (đáy bằng nhau, chung đường cao)
Tương tự: \({S_3} = {S_4}\)
\( \Rightarrow {S_2} + {S_3} = {S_1} + {S_4} = {1 \over 2}{S_{ABCD}}.\)
Hay \({S_{MBND}} = {1 \over 2}{S_{ABCD}}.\)
Bài 3.
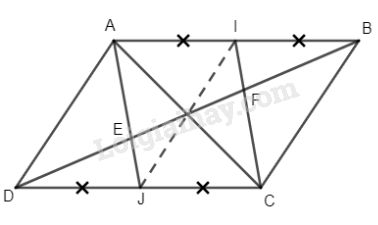
a) Ta có: \(AB// CJ\) và AI = CJ nên AICJ là hình bình hành.
b) Ta nối đường chéo AC ta có:
\({S_{ADJ}} = {S_{ACJ}} = {S_{ACI}} = {S_{BCI}}\) do đó
\({S_{ACJ}} + {S_{ACI}} = {S_{ADJ}} + {S_{BCI}} = {1 \over 2}{S_{ABCD}}\)
Hay \({S_{AICJ}} = {1 \over 2}{S_{ABCD}} = 24c{m^2}\).
c) Ta có \(IF//AE\) và I là trung điểm của AB (gt) nên IF là đường trung bình của \(\Delta ABE\) nên F là trung điểm của EB hay FE = FB.
Tương tự ta có E là trung điểm của DF nên FD = EF.
Vậy DE = EF = FB hay BD = 3DE.
Chú ý: Các bạn có thể giải câu c) bài 3 bằng cách khác: ta có E, F là trọng tâm các tam giác ACD và ABC.






