
Bài 1. Tính diện tích hình vuông biết đường chéo là 8 cm.
Bài 2. Trên cạnh DC của hình bình hành ABCD lấy một điểm E. Gọi I là giao điểm của AE và đường chéo BD.
Chứng minh rằng: \({S_{ABE}} – {S_{DIE}} = {S_{BIEC}}.\)
Bài 3. Cho tam giác ABC, trên tia AB lấy điểm D sao cho BD = 3DA. Trên BC lấy điểm E sao cho \(BE = 4EC.\) Gọi F là giao điểm của AE và CD.
a) Chứng minh FD = FC.
b) Chứng minh \({S_{ABC}} = 2{S_{AFB}}.\)

Bài 1.
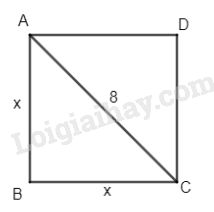
Gọi cạnh hình vuông là x, ta có \(\Delta ABC\) vuông cân cạnh x.
Advertisements (Quảng cáo)
\({x^2} + {x^2} = {8^2}\) (định lý Py – ta – go)
\( \Rightarrow 2{x^2} = 64 \Rightarrow {x^2} = 32\) \( \Rightarrow x = \sqrt {32} \left( {cm} \right)\)
Vậy \({S_{ABCD}} = {x^2} = {\left( {\sqrt {32} } \right)^2} = 32\left( {c{m^2}} \right).\)
Bài 2.
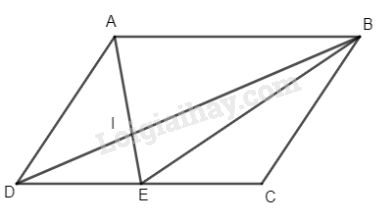
Ta có AB = CD (gt)
Advertisements (Quảng cáo)
\( \Rightarrow {S_{AEB}} = {S_{BDC}}\) (hai đáy bằng nhau, hai đường cao tương ứng bằng nhau)
Mà \({S_{BDC}} – {S_{DIE}} = {S_{BIEC}}\)
Do đó: \({S_{ABE}} – {S_{DIE}} = {S_{BIEC}}.\)
Bài 3.
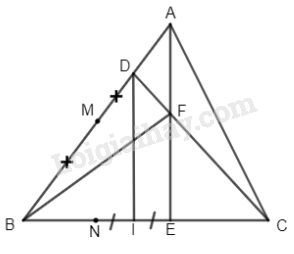
a) Gọi M là trung điểm của AB và N là trung điểm của BE
\( \Rightarrow D\) là trung điểm của MA.
Gọi I là trung điểm của NE. Khi đó \(DI// AE.\)
Trong \(\Delta CDI\) có E là trung điểm IC và \(EF//DI\) nên F là trung điểm của CD (đường trung bình của tam giác) hay FD = FC.
b) Ta có: \({S_{AFB}} = {S_{AFD}} + {S_{DFB}}\)
mà \({S_{AFD}} = {1 \over 2}{S_{ADC}}\) (vì F là trung điểm của DC)
và \({S_{DFB}} = {1 \over 2}{S_{BCD}}\) (vì F là trung điểm DC)
\( \Rightarrow {S_{AFD}} + {S_{DFB}} = {1 \over 2}\left( {{S_{ADC}} + {S_{BCD}}} \right)\)
\( \Rightarrow {S_{AFB}} = {1 \over 2}{S_{ABC}}.\)
Do đó: \({S_{ABC}} = 2{S_{AFB}}.\)






