Bài 1. Cho hình thoi MNPQ. Gọi O là giao điểm của hai đường chéo. Kẻ \(NE \bot PQ\left( {E \in PQ} \right),\) \(QF \bot MN\left( {F \in MN} \right).\)
a) Chứng tỏ tứ giác NEQF là hình chữ nhật.
b) Chứng tỏ MP, NQ, EF đồng quy.
Bài 2. Cho hình chữ nhật ABCD có AB = 2AD. Vẽ BH vuông góc với AC. Gọi M, N, P lần lượt là trung điểm của AH, BH và CD.
a) Chứng minh tứ giác MNCP là hình bình hành.
b) Chứng minh rằng: \(MP \bot MB.\)
c) Gọi I là trung điểm của PB và J là giao điểm của MC và NP. Chứng minh rằng: \(MI – {\rm{IJ}} < JP.\)
Bài 1.
Advertisements (Quảng cáo)
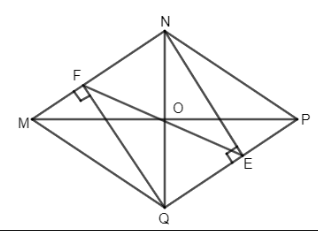
a) Ta có \(NF\parallel QE(gt),\) QF và NE lần lượt vuông góc với MN và PQ mà \(MN\parallel PQ\) nên \(QF\parallel NE.\) Do đó tứ giác NEQF là hình bình hành có một góc vuông nên là hình chữ nhật.
b) Gọi O là giao điểm hai đường chéo hình thoi MNPQ nên O là trung điểm của NQ.
Lại có NEPQ là hình chữ nhật (cmt) nên đường chéo EF phải qua trung điểm O của NQ. Vậy MP, NQ, EF đồng quy.
Bài 2.
Advertisements (Quảng cáo)
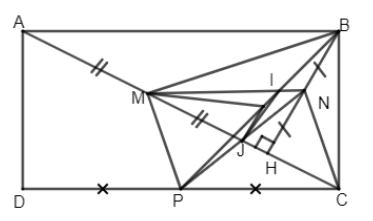
a) Ta có M là trung điểm của HA (gt), N là trung điểm của HB (gt) nên MN là đường trung bình của \(\Delta AHB\)
\( \Rightarrow MN\parallel AB\) và \(MN = {1 \over 2}AB,P\) là trung điểm của CD.
Do đó \(MN\parallel CP\) và MN = CP, vậy tứ giác MNCP là hình bình hành.
b) Ta có \(MN\bot PC\) cmt
Mà \(PC\bot BC\Rightarrow MN\bot PC\)
Chứng tỏ N là trực tâm của tam giác AMC
\(\Rightarrow CN \bot MB\)
Mà CN// MP (cmt) \(\Rightarrow MP \bot MB.\)
c) \(\Delta BMP\) vuông (cmt) có MI là trung tuyến nên \(MI = IP = {1 \over 2}BP.\)
Xét \(\Delta {\rm{IJ}}P\) theo bất đẳng thức tam giác có:
\(JP + {\rm{IJ}} > IP\) hay \(JP + {\rm{IJ}} > MI \Rightarrow MI – {\rm{IJ}} < JP\) (đpcm).
