Kiểm tra 15 phút Toán – Chương 1 Hình học 8: Chứng minh rằng Δ BAE = Δ CAD

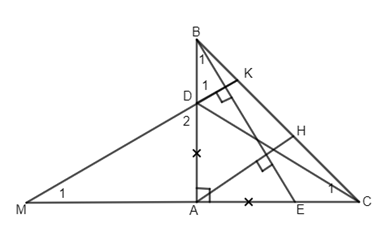
Cho tam giác ABC vuông  cân tại A. Trên các cạnh góc vuông AB, AC lấy D và E sao cho AD = DE. Qua D vẽ đường thẳng vuông góc với BE cắt BC ở K. Qua A vẽ đường thẳng vuông góc với BE cắt BC ở H. Gọi M là giao điểm của DK và AC. Chứng minh rằng:

a) \(\Delta BAE = \Delta CAD\)

b) \(\Delta MDC\) cân

c) \(HK = HC.\)

a) Xét hai tam giác vuông  \(\Delta BAE \) và \( \Delta CAD\) có:

+) AB = AC (gt)

+) AE = AD (gt)

Suy ra \(\Delta BAE = \Delta CAD \) (c.c.c)

b) Ta có \(\widehat {{D_1}} = \widehat {{D_2}}\) (đối đỉnh) \( \Rightarrow \widehat {{B_1}} = \widehat {{M_1}}\) (cùng phụ với \(\widehat {{D_1}}\) và \(\widehat {{D_2}}\) )

Mà \(\widehat {{B_1}} = \widehat {{C_1}}\) (cmt)

\( \Rightarrow \widehat {{M_1}} = \widehat {{C_1}}\) hay \(\Delta MDC\) cân tại D.

c) \(\Delta MDC\) cân tại D nên đường cao DA đồng thời là đường trung tuyến hay A là trung điểm của MC.

Lại có \(AH// MK \bot BE.\)

Do đó AH là đường trung bình của \(\Delta MCK \Rightarrow H\) là trung điểm của KC hay HK = HC.