Đề kiểm tra 1 tiết Chương 4 – Hình trụ – Hình nón – Hình cầu Hình học lớp 9: Tính thể tích của hình khối sinh ra do ∆CID quay quanh CD.

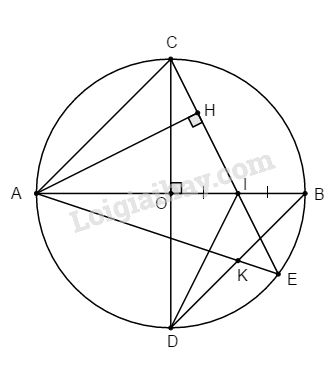
AB và CD là hai đường kính vuông góc của đường tròn (O; R). Kẻ dây CE qua trung điểm I của bán kính OB, kẻ đường cao AH của ∆ACE.

a)  Tính CE, AH và diện tích ∆ACE theo R.

b)  Chứng minh đường tròn qua ba điểm A, I, E tiếp xúc với đường thẳng AC.

c)  Gọi K là giao điểm của AE và BD. Chứng minh: \(AK.AE + BK.BD = 4R^2\)

d)  Tính thể tích của hình khối sinh ra do ∆CID quay quanh CD.

a) ∆COI vuông tại O (gt), ta có :

\(CI = \sqrt {C{O^2} + O{I^2}}  = \sqrt {{R^2} + {{\left( {{R \over 2}} \right)}^2}}\)\(\;  = {{R\sqrt 5 } \over 2}\)

\( \Rightarrow cos\widehat {OCI} = {{OC} \over {CI}} = {R \over {{{R\sqrt 5 } \over 2}}} = {{2\sqrt 5 } \over 5}\)

Lại có ∆CED vuông ( CD là đường kính) nên

\(CE = CD.cos\widehat {OCI} = 2R.{{2\sqrt 5 } \over 5} \)\(\;= {{4R\sqrt 5 } \over 5}\)

Xét hai tam giác vuông AHI và COI có \(\widehat {HAI} = \widehat {OCI}\) ( cùng phụ với \(\widehat {OIC}\))

Do đó ∆AHI và ∆COI đồng dạng (g.g) \( \Rightarrow {{AH} \over {CO}} = {{AI} \over {CI}}\)

\( \Rightarrow AH = {{CO.AI} \over {CI}} = \left( {R.{{3R} \over 2}} \right):{{R\sqrt 5 } \over 2}\)\(\; = {{3\sqrt 5 R} \over 5}\)

Vậy \({S_{ACE}} = {1 \over 2}AH.CE = {1 \over 2}.{{3\sqrt 5 R} \over 5}.{{4R\sqrt 5 } \over 5}\)\(\; = {{6{R^2}} \over 5}\).

b)    Ta có \(AB \bot  CD\) (gt)  mà \(\widehat {CBA} = \widehat {CEA}\) ( góc nội tiếp cùng chắn )

\( \Rightarrow \widehat {CAB} = \widehat {CEA}\) hay \(\widehat {CAI} = \widehat {IEA}\)

Do đó AC là tiếp tuyến của đường tròn đi qua ba điểm A, I, E.

c) Xét ∆AIE và ∆AKB có \(\widehat {IAE}\) chung và \(\widehat {AEI} = \widehat {ABD}\) ( vì ) nên ∆AIE và ∆AKB đồng dạng (g.g) \( \Rightarrow {{AK} \over {AI}} = {{AB} \over {AE}}\) \(\Rightarrow AK.AE = AI.AB\)          (1)

Tương tự ∆BKA và ∆BID (g.g)  \( \Rightarrow {{BK} \over {BI}} = {{AB} \over {DB}}\) \(\Rightarrow BK.BD = AB.BI \)      (2)

Cộng (1) và (2), ta có : \(AK.AE + BK.BD = AB(AI + BI) \)\(\,=AB^2= 4R^2\).

d)  Khi tam giác CID quay quanh CD ta có thể tích hình sinh ra gồm hai hình nón bằng nhau và có chung đáy, bán kính \(OI = {R \over 2}\) và chiều cao OC.

Gọi V_n là thể tích của hình nón, ta có :

\({V_n} = {1 \over 3}\pi {R^2}h = {1 \over 3}\pi .{\left( {{R \over 2}} \right)^2}R = {{\pi {R^3}} \over {12}}\)

\(\Rightarrow 2V = {{\pi {R^3}} \over 6}\)