Bài 1: Cho hình chữ nhật ABCD có \(AB = a, BC = 2a\). Tính diện tích toàn phần và thể tích hình tạo ra khi quay tam giác ABC một vòng quanh AD.
Bài 2: Chi tiết máy có dạng như hình vẽ.
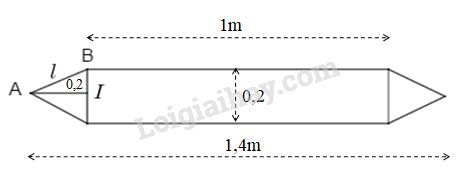
Tính diện tích bề mặt và thể tích của chi tiết đó.
Bài 1:
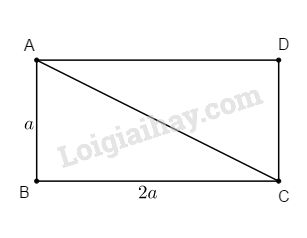
∆ADC vuông tại D, có : \(AD = BC = 2a\) và \(DC= AB = a.\)
Advertisements (Quảng cáo)
\( \Rightarrow AC = \sqrt {A{D^2} + D{C^2}} \)\(\; \sqrt {{{\left( {2a} \right)}^2} + a} = a\sqrt 5 \)
Diện tích toàn phần của hình được tạo ra bằng tổng của diện tích hình tròn bán kính AB với diện tích xung quanh hình trụ có đường sinh BC và diện tích xung quanh hình nón có đường sinh AC.
\({S_{tp}} = \pi A{B^{2}} + 2\pi AB.BC + \pi DC.AC\)
\(\;\;\;\;\;=\pi {a^2} + 4\pi {a^2} + \pi a.a\sqrt 5 \)
\(\;\;\;\;\;= \pi {a^2}\left( {5 + \sqrt 5 } \right)\)
Vì \(∆ABC = ∆ACD\) nên hình tạo bởi ∆ABC khi quay xung quanh AD có cùng thể tích với hình tạo bởi ∆ADC khi quay xung quanh AD. Đó là một hình nón và có thể tích :
Advertisements (Quảng cáo)
\({V_n} = {1 \over 3}\pi {R^2}h = {1 \over 3}\pi {a^2}.2a = {{2\pi {a^3}} \over 3}\).
Bài 2: Hình trụ có chiều cao 1m và bán kính đáy là \(0,2m : 2 = 0,1m\). Hai hình nón bằng nhau có bán kính đáy là 0,1m và có chiều cao là 0,2m, đường sinh \(AB = l.\)
Ta có : \(l = AB = \sqrt {A{I^2} + I{B^2}} \)\(\;= \sqrt {{{\left( {0,2} \right)}^2} + {{\left( {0,1} \right)}^2}} = \sqrt {0,05} \left( m \right)\)
Gọi diện tích xung quanh của hình nón : \({S_n} = \pi Rl = \pi .0,1.\sqrt {0,05} \) và diên tích xung quanh của hình trụ : \({S_t} = 2\pi Rh = 2\pi .0,1.1\)
Diện tích bề mặt :
\(S = {S_t} + 2{S_n} \)\(= 2\pi .0,1 + 2\pi .0,1\sqrt {0,05} \)
\(=0,2\pi \left( {1 + \sqrt {0,05} } \right)\left( {{m^2}} \right)\)\(\; \approx 0,768\left( {{m^2}} \right)\)
Gọi thể tích hình trụ : \({V_t} = \pi {R^2}h = \pi {\left( {0,1} \right)^2}.1\) và thể tích hình nón : \({V_n} = {1 \over 3}\pi {R^2}h = {1 \over 3}\pi {\left( {0,1} \right)^2}.0,2\)
\(\Rightarrow 2{V_n} = {2 \over 3}\pi {\left( {0,1} \right)^2}.0,2\)
Vậy thể tích của chi tiết máy :
\(V = {V_t} + 2{V_n} \)
\(\;\;\;\;= \pi {\left( {0,1} \right)^2} + {2 \over 3}\pi {\left( {0,1} \right)^2}.0,2 \)
\(\;\;\;\;= 0,01\pi \left( {1 + {{0,4} \over 3}} \right) \approx 0,036\left( {{m^3}} \right)\).
