Kiểm tra 45 phút (1 tiết) Đề số 2 Chương 2 Đường tròn Hình học 9: Chứng minh KI là tiếp tuyến của (O). Tính IK theo R.

Cho đường tròn (O; R) và điểm A nằm ngoài (O) sao cho \(OA = 2R\). Vẽ tiếp tuyến AB với (O). Gọi BH là đường cao của ∆ABO. BH cắt (O) tại C.

a. Chứng minh AC là tiếp tuyến của (O)

b. Từ O vẽ đường thẳng vuông góc với OB cắt AC tại K. Chứng minh \(KA = KO\).

c. Đoạn OA cắt đường tròn (O) tại I. Chứng minh KI là tiếp tuyến của (O). Tính IK theo R.

d. AI cắt đường tròn (O) tại điểm thứ hai D. Chứng minh ∆AIC và ∆ACD đồng dạng rồi suy ra tích \(AI.AD\) không đổi.

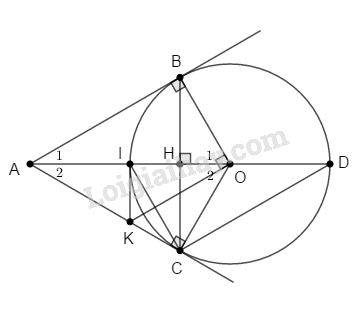
a. Ta có: \(OB = OC\; (=R)\) nên ∆BOC cân tại O có đường cao OH đồng thời là đường phân giác hay \({\widehat O_1} = {\widehat O_2}\)

Xét ∆OCA và ∆OBA có:

+) \(OA\) cạnh chung

+) \({\widehat O_1} = {\widehat O_2}\) (cmt)

+) \(OC = OB\; (= R)\)

Vậy \(∆OCA = ∆OBA\) (c.g.c)

\( \Rightarrow \widehat {OCA} = \widehat {OBA} = 90^\circ \)

\(⇒ AC\) là tiếp tuyến của (O)

b. Ta có: \(KO ⊥ OB, AB ⊥ OB\) (gt) \(⇒ KO // AB\)

\( \Rightarrow \widehat {KOA} = \widehat {BAO}\) (so le trong)

mà \(\widehat {BAO} = \widehat {KAO}\) (tính chất hai tiếp tuyến cắt nhau)

\( \Rightarrow \widehat {KOA} = \widehat {KAO} \Rightarrow KA = KO\)

c. ∆AKO cân (cmt) có KI là đường trung tuyến \(\left( {IA = IO = {{AO} \over 2} = {{2R} \over 2} = R} \right)\) nên đồng thời là đường cao hay \(KI ⊥ AO\). Chứng tỏ KI là tiếp tuyến của (O).

∆ABO vuông tại B có \(OA = 2R, OB = R\) (gt) nên là nửa tam giác đều

\( \Rightarrow {\widehat A_1} = 30^\circ  \Rightarrow {\widehat A_2} = {\widehat A_1} = 30^\circ \) (tính chất tiếp tuyến cắt nhau)

∆AKI có \({\widehat A_2} = 30^\circ ,AI = R\) nên ta có \(IK = AI.\tan 30^\circ  = {{R\sqrt 3 } \over 3}\)

d. ∆ACO vuông tại C, ta có:

\(AC = \sqrt {A{O^2} – O{C^2}} \)\(\; = \sqrt {{{\left( {2R} \right)}^2} – {R^2}}  = R\sqrt 3 \)

Xét ∆AIC và ∆ACD có \(\widehat {CAI}\) chung và \({{AI} \over {AC}} = {{AC} \over {AD}} = {1 \over {\sqrt 3 }}\) nên:

∆AIC đồng dạng ∆ACD (c.g.c) \( \Rightarrow AI.AD = A{C^2} = {\left( {R\sqrt 3 } \right)^2} = 3{R^2}\) không đổi.

Cách khác: Ta có \(\widehat {ICO} = \widehat {DIC} \Rightarrow \widehat {ACI} = \widehat {ADC}\) ⇒ ∆AIC đồng dạng ∆ACD (g.g)