Giới thiệu đề thi kì 1 toán 8 có đáp án năm 2017 – Tam Đảo, Vĩnh Phúc

Dưới đây là Đáp án đề thi học kì 1 lớp 8 Toán của phòng GD&ĐT Tam Đảo – Vĩnh Phúc năm học 2017 – 2018. Đề thi khá hay vừa được tổ chức thi ngày 23/12/2017, mời các em tham khảo.

PHÒNG GD& ĐT TAM ĐẢO

ĐỀ KIỂM TRA HỌC KỲ 1 NĂM HỌC 2017 – 2018 MÔN: TOÁN 8 Thời gian làm bài: 90 phút (không kể thời gian phát đề) (Đề này gồm 1 trang)

I. TRẮC NGHIỆM (3,0 điểm):

Khoanh tròn chữ cái đứng trước câu trả lời đúng trong các câu sau:

Câu 1. Khai triển hằng đẳng thức (x- 2y)² ta được:

A. x² + 2xy + 4y²         B. x² – 4xy + 4y²

C. x² – 4xy + y²          D. x² – 4xy +2y²

Câu 2. Kết quả của phép tính 15x²y²z : (3xyz) bằng:

A. 5xyz          B. 5x²y²z           C. 15xy           D. 5xy

Câu 4. Với x = 105 thì giá trị của biểu thức x² – 10x +25 bằng:

A. 1000   B. 10000        C. 1025        D. 10025

Câu 5. Tam giác ABC vuông tại A vuông có 2 cạnh góc vuông là 6 cm và 8 cm. Độ dài trung tuyến AM bằng:

A. 10 cm    B. 7 cm          C. 5 cm            D. 8 cm.

Câu 6. Tứ giác nào luôn có hai đường chéo bằng nhau:

A. Hình thang       B. Hình chữ nhật

C. Hình thoi           D. Hình bình hành

II. TỰ LUẬN (7,0 điểm):

Câu 7 (1,5 điểm). Phân tích các đa thức sau thành nhân tử:

a) 10x + 15y     b) x² – y² – 12x+ 12y     c) x² – y² +2x +1.

Câu 8 (1,0 điểm). Thực hiện phép tính:

a) 4x (3x² – 4xy + 5y²)

b) (6x⁴y³ – 15x³y² + 9x²y²) : 3xy

Câu 9 (2,0 điểm). Cho biểu thức:

a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định?

b) Rút gọn biểu thức A.

c) Tính giá trị của biểu thức A tại x = 1.

Câu 10 (2,0 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.

a) Chứng minh tứ giác MDHE là hình chữ nhật.

b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.

c) Tam giác MNP cần có thêm điều kiện gì để DE=2EA?

Câu 11 (0,5 điểm). Cho a + b = 1, tính giá trị của biểu thức sau:

M = a³ + b³ + 3ab(a² + b²) + 6a²b²(a + b).

——– HẾT ———

ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI

I. TRẮC NGHIỆM: Mỗi câu đúng cho 0,5 điểm.

Câu	1	2	3	4	5	6
Đáp án	B	A	D	B	C	B

II. TỰ LUẬN:

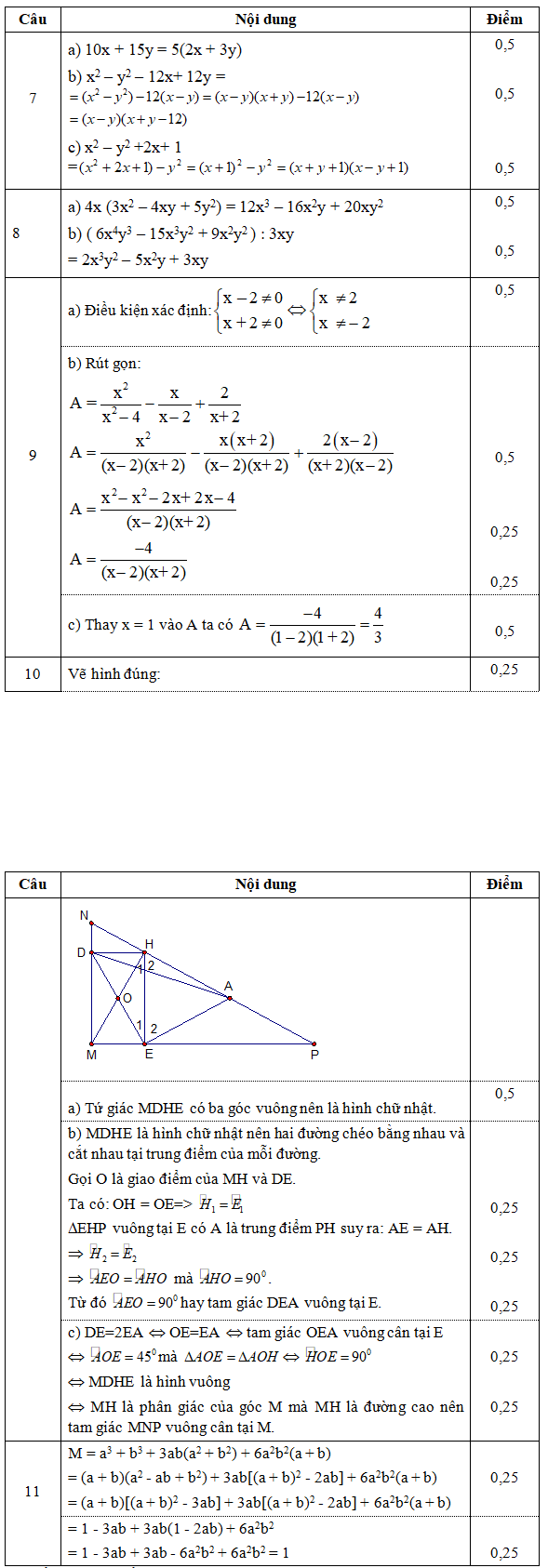
———– HẾT ————-