Đáp án và Hướng dẫn Giải bài tập 4,5,6,7 trang 10 SGK đại số 10 ( Bài tập mệnh đề)- Chương 1 mệnh đề tập hợp.
Xem bài tập trước: Giải Bài 1,2,3 trang 9 SGK Đại số lớp 10 : Bài tập mệnh đề
Bài 4. Phát biểu mỗi mệnh đề sau, bằng cách sử dụng khái niệm “điều kiện cần và đủ”
a) Một số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và ngược lại.
b) Một hình bình hành có các đường chéo vuông góc là một hình thoi và ngược lại.
c) Phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương.
Giải: a) Điều kiện cần và đủ để một số chia hết cho 9 là tổng các chữ số của nó chia hết cho 9.
b) Điều kiện cần và đủ để tứ giác là hình thoi là tứ giác là hình bình hành có hai đường chéo vuông góc với nhau.
c) Điều kiện cần và đủ để phương trình bậc hai có hai nghiệm phân biệt là biệt thức của nó dương.
Bài 5. Dùng kí hiệu ∀, ∃ để viết các mệnh đề sau
a) Mọi số nhân với 1 đều bằng chính nó;
b) Có một số cộng với chính nó bằng 0;
Advertisements (Quảng cáo)
c) Mọt số cộng vớ số đối của nó đều bằng 0.
Giải: a)∀x ∈ R: x.1=x;
b) ∃ x ∈ R: x+x=0;
c) ∀x∈ R: x+(-x)=0.
Bài 6. Phát biểu thành lời mỗi mệnh đề sau và xét tính đúng sai của nó
a) ∀x ∈ R: x2>0;
b) ∃ n ∈ N: n2=n;
Advertisements (Quảng cáo)
c) ∀n ∈ N: n ≤ 2n;
d) ∃ x∈R: x< 1/x
Giải: a) ∀x ∈ R: x2>0= “Bình phương của một số thực là số dương”. Sai vì 0∈R mà 02=0.
b) ∃ n ∈ N: n2=n = “Có số tự nhiên n bằng bình phương của nó”. Đúng vì 1 ∈ N, 12=1.
c) ∀n ∈ N: n ≤ 2n = “Một số tự nhiên thì không lớn hơn hai lần số ấy”. Đúng.
d) ∃ x∈R: x< 1/x = “Có số thực x nhỏ hơn nghịch đảo của nó”. Mệnh đề đúng. chẳng hạn 0,5 ∈ R và 0,5 <1/0,5
Bài 7. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai cuả nó.
a) ∀n ∈ N: n chia hết cho n;
b) ∃x ∈ Q: x2=2;
c) ∀x ∈ R: x< x+1;
d) ∃x ∈ R: 3x=x2+1;
Hướng dẫn:
a) Có một số tự nhiên n không chia hết cho chính nó. Mệnh đề này đúng vì n=0 ∈ N, 0 không chia hết cho 0.
b) ![]() = “Bình phương của một số hữu tỉ là một số khác 2”. Mệnh đề đúng.
= “Bình phương của một số hữu tỉ là một số khác 2”. Mệnh đề đúng.
c) ![]() = ∃x ∈ R: x≥x+1= “Tồn tại số thực x không nhỏ hơn số ấy cộng với 1”. Mệnh đề này sai.
= ∃x ∈ R: x≥x+1= “Tồn tại số thực x không nhỏ hơn số ấy cộng với 1”. Mệnh đề này sai.
d) ![]() = ∀x ∈ R: 3x ≠ x2+1= “Tổng của 1 với bình phương của số thực x luôn luôn không bằng 3 lần số x”
= ∀x ∈ R: 3x ≠ x2+1= “Tổng của 1 với bình phương của số thực x luôn luôn không bằng 3 lần số x”
Đây là mệnh đề sai vì với x=![]() ta có :
ta có :
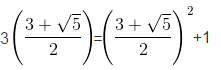





![Thi học kì 2 [Lịch sử 10]: Hãy cho biết bức tranh biếm họa bên phản ánh hiện thực gì của nước Pháp trước năm 1789?](https://dethikiemtra.com/wp-content/uploads/2019/04/mon-lich-su-lop10-100x75.jpg)
