Thầy cô và các em tham khảo tài liệu dưới đây: Đề thi học kì 1 môn Toán 9 có đáp án của SỞ GD&ĐT Vĩnh Phúc năm học 2016.
Đề thi gồm có 9 câu có trắc nghiệm và tự luận, thời gian làm bài 90 phút.
ĐỀ CHÍNH THỨC – MÃ ĐỀ 256
A. PHẦN TRẮC NGHIỆM: (2,0 điểm)
Viết phương án đúng(A, B, C hoặc D) vào bài thi.
1. Điều kiện xác định của biểu thức:
2. Giá trị của biểu thức B = 2 √(-2)2 – 3 √9 bằng
| A. -5 | B.5 |
C.-13 |
D.13 |
3. Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm. Khi đó độ dài đường cao AH bằng
| A. 1,2 cm | B.4,8 cm |
C.9,6 cm |
D.2,4 cm |
4. Cho đường tròn (O; R), dây AB = 8cm. Khoảng cách từ tâm O đến dây AB bằng 3cm. Khi đó độ dài bán kính R bằng
Advertisements (Quảng cáo)
A. 4cm
B.√7cm C.√55cm
D.5cm
B.PHẦN TỰ LUẬN: (8,0 điểm)
5 (2,0 điểm)
b) Tìm x, biết: √(x-1) = 4
6 (1,5 điểm). Cho biểu thức
Advertisements (Quảng cáo)
a) Tìm điều kiện xác định và rút gọn biểu thức P.
b) Với x thỏa mãn điều kiện xác định của P, chứng minh rằng P < 2.
7(1,5 điểm). Cho hàm số y = (m-3)x + 3 (*).
a) Tìm các giá trị của m để hàm số (*) nghịch biến trên R.
b) Tìm các giá trị của m để đồ thị của hàm số (*) song song với đường thẳng y = 4x + 4
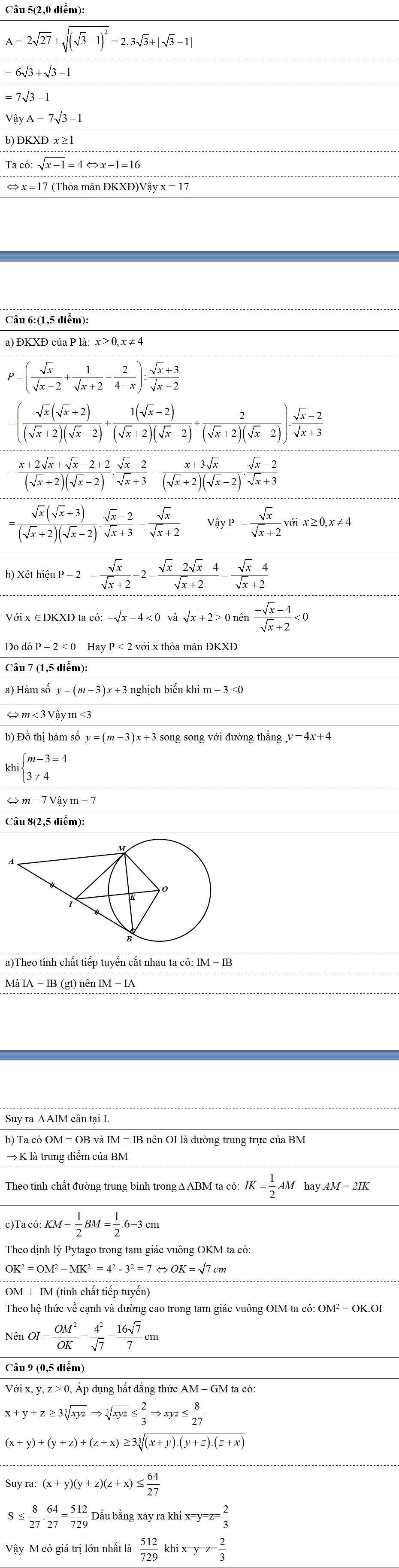
8 (2,5 điểm).Từ một điểm A ở ngoài đường tròn (O; R), kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Gọi I là trung điểm của đoạn thẳng AB, kẻ tiếp tuyến IM (M là tiếp điểm) với đường tròn (O).
a) Chứng minh rằng tam giác AIMcân.
b) Gọi K là giao điểm của OI và BM. Chứng minh rằngAM = 2IK.
c) Tính OI biết R= 4cm, BM= 6cm.
9 (0,5 điểm).Tìm giá trị lớn nhất của biểu thức M = xyz(x + y)(y + z)(z + x). Với x, y, z là các số thực dương và x + y + z = 2
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI


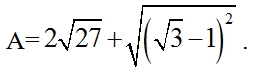
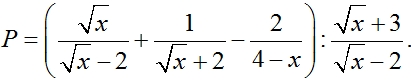


![[Trường THCS Phú Lương] kiểm tra học kì 2 môn Văn lớp 9: Sự thật là Bác đã ra đi nhưng nhà thơ lại viết “giấc ngủ bình yên”. Em hãy cho biết tác dụng của cách viết ấy?](https://dethikiemtra.com/wp-content/uploads/2020/09/tha-ho-giat-tit-cau-view-hinh-anh-thay-co-tro-thanh-dao-phu-b5a87c-100x75.jpg)



