
Bài 1 (1,0đ): Giải phương trình \({x^2} + 28x – 128 = 0\)
Bài 2 (1,5đ): Cho phương trình \((m + 1){x^2} – (2m + 3)x + m + 4 = 0\,\,\,\,\,(1)\), với \(m\) là tham số.
a) Giải phương trình khi \(m = – 1\) .
b) Tìm tất cả các giá trị của \(m\) để phương trình (1) có nghiệm.
Bài 3 (3,0đ): Cho \((P)\) là đồ thị hàm số \(y = – \dfrac{1}{2}{x^2},\,\,\,(d)\) là đồ thị hàm số \(y = 2x\) và \((d’)\) là đồ thị hàm số \(y = – x\).
a) Vẽ đồ thị của các hàm số \(y = – \dfrac{1}{2}{x^2},\,\,\,y = 2x,\,\,\,y = – x\) trên cùng một mặt phẳng tọa độ.
b) Các đồ thị \((P),\,\,(d)\,\)và \(\,(d’)\) có một điểm chung là gốc tọa độ\(O\). Gọi \(A\) là giao điểm thứ hai của \((P)\) và \((d)\), gọi \(B\) là giao điểm thứ hai của \((P)\) và \((d’)\). Chứng minh rằng tam giác \(OAB\) vuông và tính diện tích tam giác \(OAB\) (đơn vị đo trên các trục tọa độ là xentimét).
Bài 4 (1,0đ): Tìm hai số tự nhiên, biết rằng hiệu của số lớn và số nhỏ bằng \(1814\) và nếu lấy số lớn chia cho số nhỏ thì được thương là \(9\) và số dư là \(182\).
Bài 5 (3,5đ): Cho góc \(\widehat {xAy} = {60^0}\) và \((O)\) là đường tròn tiếp xúc với tia \(Ax\) tại \(B\) và tiếp xúc với tia \(Ay\) tại \(C\). Trên cung nhỏ của đường tròn \((O)\) lấy điểm \(M\) và gọi \(D,\,\,E,\,\,F\) lần lượt là hình chiếu vuông góc của \(M\) trên \(BC,\,\,CA,\,\,AB\).
a) Chứng minh tứ giác \(CDME\) là tứ giác nội tiếp.
b) Tính số đo của góc \(\widehat {EDF}\).
c) Chứng minh rằng \(M{D^2} = ME.MF\).

Bài 1: Ta có: \(\Delta ‘ = {14^2} – 1.( – 128) = 196 + 128 = 324 = {18^2}\)
\( \Rightarrow \Delta ‘ > 0\) nên phương trình có hai nghiệm phân biệt:
\({x_1} = \dfrac{{ – 14 – 18}}{1} = – 32\) và \({x_2} = \dfrac{{ – 14 + 18}}{1} = 4\)
Vậy tập nghiệm của phương trình đã cho là \(S = {\rm{\{ }} – {\rm{32; 4\} }}\)
Bài 2: a) Khi \(m = – 1\) ta có phương trình \( – x + 3 = 0\)
Do đó, phương trình có \(1\) nghiệm là \(x = 3\).
b) Khi \(m = – 1\) theo câu a phương trình có một nghiệm.
Khi \(m \ne – 1\), phương trình đã cho là một phương trình bậc \(2\) có \(\Delta = {(2m + 3)^2} – 4(m + 1)(m + 4) = – 8m\, – 7\)
Phương trình có nghiệm \( \Leftrightarrow – 8m – 7 \ge 0\) (với \(m \ne – 1\))
Kết hợp \(2\) trường hợp trên: khi \(m \le – \dfrac{7}{8}\) thì phương trình đã cho có nghiệm.
Advertisements (Quảng cáo)
Bài 3:
Cho \((P)\) là đồ thị hàm số \(y = – \dfrac{1}{2}{x^2},\,\,\,(d)\) là đồ thị hàm số \(y = 2x\) và \((d’)\) là đồ thị hàm số \(y = – x\).
a) +) Vẽ đồ thị của hàm số \(y = – \dfrac{1}{2}{x^2}\):
Chọn \(x = 0\,\, \Rightarrow y = 0\) ;
\(x = 1\,\, \Rightarrow y = – \dfrac{1}{2}{.1^2} = \dfrac{{ – 1}}{2}\);
\(x = – 1\,\, \Rightarrow y = – \dfrac{1}{2}.{( – 1)^2} = \dfrac{{ – 1}}{2}\)
Vậy đồ thị hàm số nhận trục \(Oy\) làm trục đối xứng và đi qua các điểm \((0;\,\,0);\,\,\,\left( {1;\dfrac{{ – 1}}{2}} \right);\,\,\,\left( { – 1;\dfrac{{ – 1}}{2}} \right)\).
+) Vẽ đồ thị hàm số \(y = 2x\)
Chọn \(x = 0\,\,\, \Rightarrow y = 0\,\,\,;\,\,\,x = 1 \Rightarrow y = 2\).
Đồ thị hàm số \(y = 2x\) đi qua gốc tọa độ \((0;\,\,0)\) và điểm \((1;\,\,2)\).
+) Vẽ đồ thị hàm số \(y = – x\)
Chọn \(x = 0\,\,\, \Rightarrow y = 0\,\,\,;\,\,\,x = 1 \Rightarrow y = – 1\).
Đồ thị hàm số \(y = – x\) đi qua gốc tọa độ \((0;\,\,0)\) và điểm \((1;\,\, – 1)\).
b) +) Hoành độ giao điểm của \((P)\) và \((d)\) là nghiệm của phương trình:
Advertisements (Quảng cáo)
\(\begin{array}{l} – \dfrac{1}{2}{x^2} = 2x\\ \Leftrightarrow \dfrac{1}{2}{x^2} + 2x = 0\\ \Leftrightarrow x\left( {\dfrac{1}{2}x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\\dfrac{1}{2}x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = – 4\end{array} \right.\end{array}\)
Với \(x = – 4\,\, \Rightarrow y = – 8\)
Vậy giao điểm thứ hai của \((P)\) và \((d)\)là\(A\,( – 4;\,\, – 8)\)
+) Hoành độ giao điểm của \((P)\) và \((d’)\) là nghiệm của phương trình:
\(\begin{array}{l} – \dfrac{1}{2}{x^2} = – x\\ \Leftrightarrow – \dfrac{1}{2}{x^2} + x = 0\\ \Leftrightarrow x\left( { – \dfrac{1}{2}x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\ – \dfrac{1}{2}x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\end{array}\)
Với \(x = 2\,\, \Rightarrow y = – 2\)
Vậy giao điểm thứ hai của \((P)\) và \((d’)\)là\(B\,(2;\,\, – 2)\).
+) Ta có: \(O{A^2} = {4^2} + {8^2} = 80\,\,\,;\)\(\,\,\,\,\,O{B^2} = {2^2} + {2^2} = 8\,\,\,;\)\(\,\,\,\,A{B^2} = {(4 + 2)^2} + {(8 – 2)^2} = 72\)
\( \Rightarrow O{A^2} = O{B^2} + A{B^2}\)
\( \Rightarrow \) Tam giác \(OAB\) vuông tại \(B\)
Ta có \(OB = 2\sqrt 2 \,cm\,\,;\,\,\,AB = 6\sqrt 2 \,cm.\)
Diện tích tam giác \(OAB\) là \({S_{OAB}} = \dfrac{1}{2}OB.AB = \dfrac{1}{2}.2\sqrt 2 .6\sqrt 2 = 12\,\,(c{m^2})\)
Bài 4: Gọi \(x,\,\,y\) là hai số tự nhiên cần tìm, trong đó \(y\) là số lớn, \(x\) là số bé.
Theo đề bài ta có phương trình \(y – x = 1814\) và \(y = 9x + 182\).
Nên ta có hệ phương trình \(\left\{ \begin{array}{l}y – x = 1814\\y = 9x + 182\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}y = x + 1814\\x + 1814 = 9x + 182\end{array} \right.\\\Leftrightarrow \left\{ \begin{array}{l}8x = 1632\\y = x + 1814\end{array} \right.\,\, \Leftrightarrow \left\{ \begin{array}{l}x = 204\\y = 2018\end{array} \right.\)
Vậy hai số tự nhiên cần tìm là \(204\) và \(2018\).
Bài 5: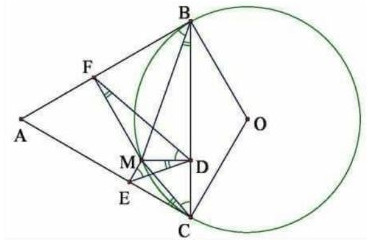
a) Ta có \(\widehat {CDM} = {90^0}\)(do \(MD \bot BC\))
\(\widehat {CEM} = {90^0}\) (do \(ME \bot AC\))
\( \Rightarrow \widehat {CDM} + \widehat {CEM} = {180^0}\)
\( \Rightarrow \)\(CDME\) là tứ giác nội tiếp.
b) Từ câu a ta có \(\widehat {MDE} = \widehat {MCE}\) (cùng chắn của đường tròn \((CDME)\))
Mà \(\widehat {MCE} = \widehat {MBC}\) (cùng chắn của đường tròn \((O)\))
\( \Rightarrow \widehat {MDE} = \widehat {MBC}\,\,\,\,(1)\)
Tương tự câu a ta cũng có tứ giác \(BDMF\) nội tiếp nên ta có:
\(\widehat {MDE} = \widehat {MBF}\,\,\,\,\,\,\,\,(2)\) (cùng chắn của đường tròn \((BDME)\))
Từ (1) và (2) ta suy ra:
\(\widehat {EDF} = \widehat {MDE} + \widehat {MDF} = \widehat {MBC} + \widehat {MBF} = \widehat {CBA} = {60^0}\) (vì tam giác \(ABC\) đều do có \(AB = AC\) và \(\widehat {BAC} = {60^0}\) )
c) Ta có \(\widehat {MED} = \widehat {MCD}\) (cùng chắn của đường tròn \((CDME)\))
Mà \(\widehat {MCD} = \widehat {MBF}\) (cùng chắn của đường tròn \((O)\))
Kết hợp (2) \( \Rightarrow \widehat {MED} = \widehat {MDF}\,\,\,\,\,\,\,\,(3)\)
Từ (1): \(\widehat {MDE} = \widehat {MBC}\)
Mà \(\widehat {MBC} = \widehat {MFD}\) (cùng chắn của đường tròn \((BDMF)\))
\( \Rightarrow \widehat {MDE} = \widehat {MFD}\,\,\,\,\,\,\,\,\,\,\,\,(4)\)
Từ (3) và (4) suy ra \(\Delta MDE\) và \(\Delta MFD\) đồng dạng
\( \Rightarrow \dfrac{{MD}}{{MF}} = \dfrac{{ME}}{{MD}}\,\, \Rightarrow M{D^2} = ME.MF\)


![[23/4] Đề và Đáp án đề thi thử vào 10 Ngữ Văn Hà Nội năm 2016](https://dethikiemtra.com/wp-content/uploads/2016/04/thi-thu-vao-lop-10-nam-2016-100x75.jpg)



