2 đề kiểm tra 1 tiết chương 1 đại số lớp 9 hay có đáp án không thể bỏ qua. Đề thi theo ma trận đề thi. Chương 1 Toán đại số 9: Căn bậc hai, căn bậc 3.
Ma trận đề kiểm tra 1 tiết chương 1 Đại số lớp 9
| CĐ -KT | Nhận Biết | Thông Hiểu | Vận Dụng | Tổng | |
| Cấp độ thấp | Cấp độ cao | ||||
| 1. Khái niệm căn bậc hai | – Xác định điều kiện có nghĩa của căn bậc hai. | – Vận dụng hằng đẳng thức √a2 = |a| để rút gọn biểu thức | – Vận dụng hằng đẳng thức √a2 = |a| để tìm x | ||
| Số câu:
Số điểm: Tỉ lệ: |
1
2 20% |
1
1 10% |
1
1 10% |
3
4 40% |
|
| 2. Các phép tính và các phép biến đổi đơn giản về căn bậc hai | – Nhân, chia căn thức bậc hai. Khai phương một tích, một thương | – Trục căn thức ở mẫu | – Biến đổi đơn giản biểu thức chứa căn bậc hai. | Tìm GTNN
Tìm GTLN Giải phương trình vô tỉ |
|
| Số câu:
Số điểm: Tỉ lệ: |
1
2 10% |
1
3 30% |
1
1 10% |
3
6 60% |
|
| Số câu:
TS điểm: 10 Tỉ lệ: 100% |
1
2 20% |
2
3 30% |
1
4 40% |
1
1 10% |
3
6 60% |
Đề kiểm tra 1 tiết Đại số 9 chương 1 – Đề số 1
Bài 1 (2điểm)
1) Nêu điều kiện để √a có nghĩa ?
2) Áp dụng: Tìm x để các căn thức sau có nghĩa:
Bài 2: ( 3 điểm ): Rút gọn biểu thức
Bài 3 ( 4 điểm ) Cho biểu thức
(Với x > 0; x 1; x4)
a/ Rút gọn P.
b/ Với giá trị nào của x thì P có giá trị bằng 1/4
c/ Tính giá trị của P tại x = 4 + 2√3
d/ Tìm số nguyên x để biểu thức P có giá trị là số nguyên ?
Bài 4 : ( 1 điểm ): Cho
Tìm giá trị nhỏ nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
Đề kiểm tra 1 tiết Đại số 9 chương 1 – Đề số 2
Bài 1: (2.0đ)
1/ Nêu điều kiện để √a có nghĩa ?
2/ Áp dụng: Tìm x để các căn thức sau có nghĩa ?
Advertisements (Quảng cáo)
Bài 2: ( 3 điểm ): Rút gọn biểu thức
Bài 3 (4điểm) Cho biểu thức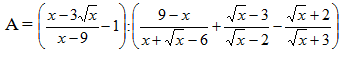 
(Với x 0; x 2; x9)
a) Rút gọn biểu thức A
b) Với giá trị nào của x thì A có giá trị bằng 1/2
c) Tính giá trị của A tại x = 19 – 8√3
d) Tìm số nguyên x để biểu thức A có giá trị là số nguyên?
Bài 4(1điểm): Cho B = x + 4√x
Tìm x để biểu thức B đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó?
Đáp án và hướng dẫn chấm Đề kiểm tra Đại 9 chương 1 số 1.
Advertisements (Quảng cáo)
Bài 1: Mỗi ý đúng được 1 điểm.
Câu 2: Mỗi ý đúng được 1 điểm.
Bài 3: 4 điểm: Mỗi ý đúng được 1 điểm
a) Rút gọn P
b) Với x > 0; x ≠ 1; x ≠ 4; P = 1/4
⇔ √x – 2/3√x = 1/4 ⇔ √4x – 8 = 3√x ⇔ √x = 8 ⇔ x = 64 (TMĐK)
Vậy với x = 64 thì P =1/4
c) Thay x = 4 + 2√3 vào biểu thức P ta có
d/ Lập luận đưa ra kết quả : Không có giá trị thích hợp của x thỏa mãn
Bài 4: (1 điểm)
Ta có x – 2√x + 3 = (√x – 1)2 + 2. Mà (√x – 1)2 ≥ 0 với mọi x ≥ 0 ⇒ (√x – 1)2 + 2 ≥ 2 với mọi x ≥ 0
⇒
Vậy GTLN của A = 1/2 ⇔ √x = 1 ⇔ x =1
Đáp án và hướng dẫn chấm Đề kiểm tra Đại 9 chương 1 số 2.
Bài 1: Mỗi ý đúng được 1 điểm.
Câu 2: Mỗi ý đúng được 1 điểm.
Bài 3: 4 điểm: Mỗi ý đúng được 1 điểm
a) Rút gọn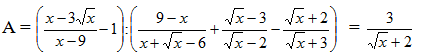 
Vậy với x = 16 thì A = 1/2
c) Thay x = 19 – 8√3 vào biểu thức ta được
Vậy với x = 19 – 8√3 thì A = (6+√3)/11
d) Tìm được x = 1 thỏa mãn đk
Bài 4: (1điểm):
B = 4√x – x = -(x – 4√x) = -(x – 4√x + 4) + 4= -(√x – 2)2 + 4 ≤ 4
Dấu = xảy ra khi và chỉ khi (√x – 2)2 = 0 hay (√x – 2) = 0 => x = 4
Vậy GTLN của B = 4 khi x = 4
