
I. TRẮC NGHIỆM (2đ)
1: Kết quả của phép tính: \(\left( {{a^2} + 2a + 4} \right)\left( {a – 2} \right)\) là:
A. \({a^3} – 8\)
B. \({\left( {a – 2} \right)^3}\)
C. \({a^3} + 8\)
D. \({\left( {a + 2} \right)^3}\)
2. : Kết quả của phép tính: \(\left( { – 2017{x^4}{y^3}} \right):\left( { – {x^3}{y^3}} \right)\) là:
A. \( – 2017x\)
B. \(2017x\)
C. \( – 2017xy\)
D. \(2017xy\)
3. : Phân tích đa thức \({x^2} – x – 6\) thành nhân tử được kết quả là:
A.\(\left( {x + 2} \right)\left( {x + 3} \right)\)
B.\(\left( {x – 2} \right)\left( {x + 3} \right)\)
C.\(\left( {x – 2} \right)\left( {x – 3} \right)\)
D.\(\left( {x + 2} \right)\left( {x – 3} \right)\)
4. : Tập hợp tất cả các giá trị của \(x\) thỏa mãn: \({x^3} = – x\) là:
A. \(\left\{ {0;\, – 1} \right\}\)
B. \(\emptyset \)
C. \(\left\{ 0 \right\}\)
D. \(\left\{ {0; \pm 1} \right\}\)
5. : Hình chữ nhật \(ABC{\rm{D}}\) có \(AB = 6\,cm,\,BC = 4\,cm\). Khi đó, diện tích hình chữ nhật ABCD là:
A. \(2\,c{m^2}\)
B. \(10\,c{m^2}\)
C. \(12\,c{m^2}\)
D. \(24\,c{m^2}\)
6. : Số lượng trục đối xứng của hình vuông là:
A. \(6\)
B. \(4\)
Advertisements (Quảng cáo)
C. \(2\)
D. \(1\)
7. : Một hình thoi có cạnh bằng \(10\,cm\)và độ dài một đường chéo là \(12\,cm\). Khi đó, độ dài đường chéo còn lại của hình thoi là:
A. \(16\,cm\)
B. \(12\,cm\)
C. \(8\,cm\)
D. \(4cm\)
8. : Tứ giác là hình vuông khi tứ giác đó có:
A. Hai đường chéo bằng nhau và vuông góc với nhau
B. Bốn cạnh bằng nhau
C. Bốn cạnh bằng nhau và có một góc vuông
D. Bốn góc vuông.
II. TỰ LUẬN (8đ)
Bài 1 (1,5đ)Phân tích các đa thức sau thành nhân tử:
a)\(2x – 4{x^2}\)
b)\(3x\left( {x – 2} \right) – 4x + 8\)
c)\({x^2} – 2xy + {y^2} – 9{{\rm{z}}^2}\)
Bài 2 (1,25đ)
a)Tìm số\(m\), biết đa thức \(2{x^3} – 3{x^2} + x + m\)chia hết cho đa thức \(x + 2\)
Advertisements (Quảng cáo)
b)Cho \(P = x – {x^2} – 1\), chứng minh \(P < 0\,\forall \,x\)
Bài 3 (1,25đ)Rút gọn các phân thức sau:
a)\(A = \dfrac{{45x\left( {2 – x} \right)}}{{15x{{\left( {x – 2} \right)}^2}}}\)
b)\(B = \dfrac{{{x^3} + 2{x^2}y – x{y^2} – 2{y^3}}}{{{x^2} + 3xy + 2{y^2}}}\)
Bài 4 (3,0đ)Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Gọi \(M,\,N\) theo thứ tự là chân các đường vuông góc kẻ từ\(H\) đến \(AB,\,AC\). Gọi \(O\) là giao điểm của \(AH\) và \(MN\),\(K\)là trung điểm của \(CH\)
a)Chứng minh rằng tứ giác \(AMHN\) là hình chữ nhật.
b)Tính số đo \(\angle MNK\)
c)Chứng minh rằng \(BO \bot AK\)
Bài 5 (1,0đ)Chứng minh: \({a^4} + {b^4} + {c^4} = 2{\left( {ab + bc + ac} \right)^2}\). Biết rằng \(a + b + c = 0\)

I. Trắc nghiệm
| 1. | 2. | 3. | 4. |
| A | B | D | C |
| 5. | 6. | 7. | 8. |
| D | B | A | B |
Tự luận
Bài 1: \(a)\,\,2x – 4{x^2} = 2x\left( {1 – 2x} \right)\)
\(b)\,\,3x\left( {x – 2} \right) – 4x + 8\)
\(= 3x\left( {x – 2} \right) – 4\left( {x – 2} \right) \)
\(= \left( {x – 2} \right)\left( {3x – 4} \right).\)
\(c)\,\,{x^2} – 2xy + {y^2} – 9{{\rm{z}}^2} \)
\(= {\left( {x – y} \right)^2} – {\left( {3{\rm{z}}} \right)^2} \)
\(= \left( {x – y – 3{\rm{z}}} \right)\left( {x – y + 3{\rm{z}}} \right).\)
Bài 2: a) Ta có:
\( \Rightarrow \left( {2{x^3} – 3{x^2} + x + m} \right) \vdots \left( {x + 2} \right) \Leftrightarrow m – 30 = 0 \Leftrightarrow m = 30\)
Vậy \(m = 30.\)
\(b)\,P = x – {x^2} – 1 = – \left( {{x^2} – x + 1} \right) \\\;\;\;= – \left( {{x^2} – 2.\dfrac{1}{2}.x + \dfrac{1}{4} + \dfrac{3}{4}} \right) \\\;\;\;= – {\left( {x – \dfrac{1}{2}} \right)^2} – \dfrac{3}{4}\)
Vì \( – {\left( {x – \dfrac{1}{2}} \right)^2} \le 0\,\forall \,x \Rightarrow – {\left( {x – \dfrac{1}{2}} \right)^2} – \dfrac{3}{4} < 0\,\forall \,x\)
Vậy \(P < 0\) với mọi \(x.\)
Bài 3: \(a)\,A = \dfrac{{45x\left( {2 – x} \right)}}{{15x{{\left( {x – 2} \right)}^2}}} = \dfrac{{3\left( {2 – x} \right)}}{{{{\left( {2 – x} \right)}^2}}} = \dfrac{3}{{2 – x}}.\)
\(\begin{array}{l}b)\,\,B = \dfrac{{{x^3} + 2{x^2}y – x{y^2} – 2{y^3}}}{{{x^2} + 3xy + 2{y^2}}} \\= \dfrac{{\left( {{x^3} + 2{x^2}y} \right) – \left( {x{y^2} + 2{y^3}} \right)}}{{{x^2} + xy + 2xy + 2{y^2}}}\\ = \dfrac{{{x^2}\left( {x + 2y} \right) – {y^2}\left( {x + 2y} \right)}}{{x\left( {x + y} \right) + 2y\left( {x + y} \right)}}\\ = \dfrac{{\left( {x + 2y} \right)\left( {{x^2} – {y^2}} \right)}}{{\left( {x + y} \right)\left( {x + 2y} \right)}}\\ = \dfrac{{\left( {x + 2y} \right)\left( {x + y} \right)\left( {x – y} \right)}}{{\left( {x + y} \right)\left( {x + 2y} \right)}} = x – y.\end{array}\)
Bài 4: 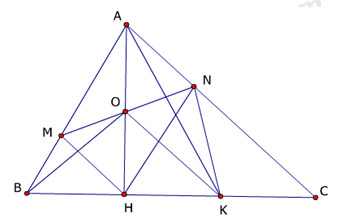
a)Vì \(M,\,N\) lần lượt là hình chiếu của \(H\) trên \(AB,\,AC\) (gt) nên \( \Rightarrow \angle HNA = \angle HMA = {90^0}\)
Lại có \(\angle MAN = {90^0}\left( {gt} \right) \Rightarrow AMHN\) là hình chữ nhật (dhnb)
b)Xét \({\Delta _v}HNC\) có K là trung điểm của \(HC\left( {gt} \right) \Rightarrow NK\) là đường trung tuyến.
Áp dụng tính chất trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy:
\( \Rightarrow NK = HK = \dfrac{{HC}}{2} \Rightarrow \Delta HKN\) cân tại K (định nghĩa)
\( \Rightarrow \angle KHN = \angle KNH\) (tính chất)
Vì \(AMHN\) là hình chữ nhật (cmt) \( \Rightarrow \angle MNH = \angle AHN\)
Lại có: \(\angle AHN + \angle NHC = {90^0} \)
\(\Rightarrow \angle MNH + \angle HNK = {90^0}\)
\(\Rightarrow \angle MNK = {90^0}\)
c)Xét \(\Delta AHC\) có \(O,\;K\) lần lượt là trung điểm của \(AH,\;\;HC \Rightarrow OK\) là đường trung bình của \(\Delta AHC.\)
\( \Rightarrow OK//AC.\)(tính chất đường trung bình)
Mà \(AC \bot AB = \left\{ A \right\}\;\;\left( {gt} \right) \Rightarrow OK \bot AB.\)
Xét \(\Delta ABK\) có \(AH,\;KO\) là các đường cao cắt nhau tại \(O \Rightarrow O\) là trực tâm của \(\Delta ABK.\)
\( \Rightarrow BO\) là đường cao của \(\Delta ABK \Rightarrow BO \bot AK.\) (đpcm)
Bài 5: Ta có:\(a + b + c = 0 \Leftrightarrow a = – b – c.\)
\(\begin{array}{l} \Rightarrow {a^2} = {\left( {b + c} \right)^2} \Leftrightarrow {a^2} = {b^2} + {c^2} + 2bc\\ \Leftrightarrow {a^2} – {b^2} – {c^2} = 2bc.\\ \Leftrightarrow \left( {{a^2} – {b^2} – {c^2}} \right) = 4{b^2}{c^2}\\ \Leftrightarrow {a^4} + {b^4} + {c^4} – 2{a^2}{b^2} + 2{b^2}{c^2} – 2{a^2}{c^2} = 4{b^2}{c^2}\\ \Leftrightarrow {a^4} + {b^4} + {c^4} = 2{a^2}{b^2} + 2{b^2}{c^2} + 2{a^2}{c^2}\\ \Leftrightarrow {a^4} + {b^4} + {c^4} = 2\left( {{a^2}{b^2} + {b^2}{c^2} + {a^2}{c^2}} \right).\end{array}\)
Lại có:
\(\begin{array}{l}\;\;\;{\left( {ab + bc + ca} \right)^2} = {\left( {ab} \right)^2} + {\left( {bc} \right)^2} + {\left( {ca} \right)^2} + 2{a^2}bc + 2a{b^2}c + 2ab{c^2}\\ \Leftrightarrow \;{\left( {ab + bc + ca} \right)^2} = {a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2} + 2abc\left( {a + b + c} \right)\\ \Leftrightarrow \;{\left( {ab + bc + ca} \right)^2} = {a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}.\\ \Rightarrow {a^4} + {b^4} + {c^4} = 2{\left( {ab + bc + ca} \right)^2}.\;\;\;\left( {dpcm} \right)\end{array}\)


![[Ba Đình – HN] Đề thi học kì 2 Toán lớp 8: Giải bất phương trình và biểu diễn nghiệm trên trục số](https://dethikiemtra.com/wp-content/uploads/2018/04/THCS-BA-DINH-100x75.jpg)



