Đề thi:
Bài 1: (2 điểm). Phân tích các đa thức sau thành nhân tử.
a) xy – 2y – x + 2
b) x² – 2xy – 9 + y²
Bài 2: (1,5 điểm). Tìm x biết.
a) x² – x – 6(x-1) = 0
b) 2x² – 2 + (2x – 1)(3 – x) = 2
Bài 3:(2,5 điểm). Cho các biểu thức
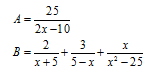
a, Tính giá trị của biểu thức A tại x = -1.
b, Rút gọn biểu thức B.
c, Tìm các giá trị nguyên của x để B:A nhận giá trị nguyên.
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, AH là đường cao. M là một điểm bất kỳ trên cạnh BC (M khác H). Gọi E, F theo thứ tự là hình chiếu của M trên cạnh AB, AC.
Advertisements (Quảng cáo)
a, Chứng minh tứ giác AEMF là hình chữ nhật.
b, Giả sử AB = 3cm, AC = 4cm. Tính BC và AH.
c, Gọi giao điểm của EF và AM là O. N là điểm đối xứng với O qua A
B.Chứng minh tứ giác ANEO là hình thoi.
d, Tính góc EHF.
Bài 5: (0,5điểm). Tìm giá trị nhỏ nhất của biểu thức P biết:
![]()
ĐÁP ÁN ĐỀ THI HỌC KÌ 1 MÔN TOÁN 8
Advertisements (Quảng cáo)
Bài 1:
| a, =(x-2)(y-1) (1đ)
b,=(x-y-3)(x-y+3) (1đ) |
Bài 2:
a, x=1; x=6 (0,75đ)
b, x = 1 (0,75đ)
Bài 3:
a) Tính đúng GTBT A là -25/12 (0,75)
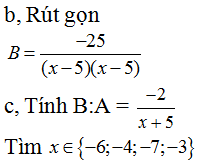
Bài 4
a, AEMF là hcn vì có 3 góc vuông
b, Vận dụng Đ/L Py-ta-go tính được BC = 5cm
Sử dụng công thức tính dt tam giác vuông tính AH = 2,4cm
c, Chứng minh ANEO là hình thoi theo dhnb
d) Tính góc EHF = 900
Vẽ hình đúng đến câu a, cho 0.25đ
a, chứng minh đúng cho 1,0đ
b, Tính đúng BC = 5cm cho 0.5đ
tính đúng AH=2.4cm cho 0,5đ
c, Chứng minh tgANEO là hình thoi theo dhnb đúng cho 0.75đ.
d, Tính góc EHF = 900 cho 0,5


![[THCS Trần Phú] thi học kì 2 môn Sử lớp 8 năm 2020: Vẽ sơ đồ tổ chức bộ máy nhà nước cai trị của Pháp Ở Đông Dương?](https://dethikiemtra.com/wp-content/uploads/2020/06/sử-100x75.jpg)
![[THCS Hồng Dương] kiểm tra cuối năm môn Địa lớp 8: Vì sao tính chất nhiệt đới của miền Bắc và Đông Bắc Bắc Bộ bị giảm sút mạnh mẽ?](https://dethikiemtra.com/wp-content/uploads/2020/09/hinh-anh-dep-co-giao-dang-giang-bai_015649158-100x75.jpg)


