1. Điều tra về số con của 20 hộ gia đình trong tổ dân phố ta có số liệu sau :
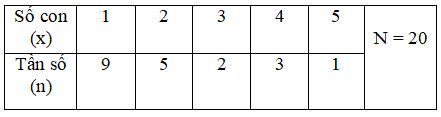
Mod của dấu hiệu là:
A. 9 B. 5
C. 1 D. 20
2. Bộ ba nào sau đây là ba cạnh của một tam giác ?
A. 3; 4; 6 B. 3; 3; 6
C. 2; 3; 6 D. 2; 4; 6
3. Tích của hai đơn thức \(\dfrac{{ – 1}}{3}\)x2y2 và (-6) xy3 là:
A. -2x2y3
B. 2x2y6
C. 2x3y5
D. -2 x3y5
4. Cho đa thức x8 + 3x5y5 – y6 – 2x6y2 + 5x7 . Bậc của đa thức đối với biến x là :
A. 5 B.6
C.7 D.8
5. Cho \(\Delta KMN\) cân tại M, ta có
A. KM=KN
B. MN=MK
C. KN=MN
D. \(\hat K = {60^0}\)
6. Hai đơn thức nào đồng dạng?
A. 2x2y; 2xy2
B. 3xy2z; 3x2yz
C. -3xy2 ; 2xy2
D.3x2y2; 2xy2
7. Cho đa thức 3x5 – 7x4 + 2x2 – 5 . Số các hạng tử là:
A. 1 B. 2
C. 3 D.4
8. Cho A(x) = 7 – 4x , A(-1) =
A. 3 B. -3
C. 11 D. -11
9. Một tam giác cân có góc ở đỉnh bằng 1200 thì mỗi góc ở đáy có số đo là :
A. 600
Advertisements (Quảng cáo)
B. 300
C. 400
D. 500
1.0: Cho \(\Delta ABC\) có AB = 5cm ; BC = 8cm ; AC = 10cm. So sánh nào sau đây là đúng
A. \(\hat B < \hat C < \hat A\)
B. \(\hat C < \hat A < \hat B\)
C. \(\hat A < \hat B < \hat C\)
D. \(\hat C < \hat B < \hat A\)
1.1: Phát biểu nào sau đây là sai ?
A.Tam giác đều có ba góc đều bằng 600
B.Tam giác vuông có một góc nhọn bằng 450 là tam giác cân .
C. Hai tam giác đều thì bằng nhau.
D. Tam giác cân có cạnh đáy bằng cạnh bên là tam giác đều .
1.2: Cho \(\Delta ABC\) với I là giao điểm của ba đường phân giác . Phát biểu nào sau đây là đúng?
A. Đường thẳng AI luôn vuông góc với cạnh BC.
B. Đường thẳng AI luôn đi qua trung điểm của cạnh BC.
C. IA = IB = IC.
D. Điểm I cách đều ba cạnh của tam giác.
II/ TỰ LUẬN: (7đ) (70 phút)
Bài 1: (1,5đ) Điểm kiểm tra môn Toán của 30 học sinh lớp 7 được ghi lại như
sau:

Advertisements (Quảng cáo)
a) Dấu hiệu cần tìm hiểu ở đây là gì ?
b) Lập bảng tần số .Tính số trung bình cộng.
Bài 2: (1,5đ) Cho hai đa thức:
A(x) = \({x^5} – 3{x^2} – 5{x^4} – 9{x^3} + {x^2}\)\(\, – \dfrac{1}{4}x + 7{x^3}\) ;
B(x) = \(5{x^4} – {x^5} – {x^2} + 2{x^3} + 3{x^2} – \dfrac{1}{4}\)
a) Rút gọn rồi sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến
b) Tính A(x) + B(x)
c) Tìm nghiệm của đa thức A(x) + B(x)
Bài 3: (4đ) Cho\(\Delta ABC\) vuông tại A có AB = 6cm, AC = 8cm; đường phân giác BI. Kẻ IH\( \bot \) BC ( H \(\in\) BC). Gọi K là giao điểm của AB và IH.
a) Tính BC ?
b) Chứng minh: \(\Delta ABI = \Delta HBI.\)
c) Chứng minh: BI là đường trung trực của đoạn thẳng AH.
d) Chứng minh: IA < IC
e) Chứng minh I là trực tâm \(\Delta BKC\)

I/ TRẮC NGHIỆM: (3đ) Mỗi câu 0.25 điểm
| Câu | 1 | 2 | 3 | 4 | 5 | 6 |
| ĐA | C | A | C | D | B | C |
| Câu | 7 | 8 | 9 | 10 | 11 | 12 |
| ĐA | D | C | B | B | C | D |
II/ TỰ LUẬN: (7đ)
Bài 1: (1,5đ)
a) Dấu hiệu: Điểm kiểm tra môn Toán của 30 học sinh lớp 7
b)
|
Điểm (x) |
Tần số (n) |
Tích (xn) |
Trung bình cộng |
|
3 4 5 6 7 8 9 10 |
1 3 2 5 6 7 3 3 |
3 12 10 30 42 56 27 30 |
|
|
|
N= 30 |
Tổng: 210 |
\(\overline X\)\(\, = \dfrac{{210}}{{30}} = 7\) |
Bài 2:(1,5đ)
a) Rút gọn rồi sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến
\(A(x)={x^5} – 5{x^4} – 2{x^3} – 2{x^2} – \dfrac{1}{4}x\)
\(B(x) = – {x^5} + 5{x^4} + 2{x^3} + 2{x^2} – \dfrac{1}{4}\)
b) Tính A(x) + B(x)
\(A(x)+B(x)=\dfrac{{ – 1}}{4}x – \dfrac{1}{4}\)
c) Tìm nghiệm của đa thức A(x) + B(x)
c) Tìm nghiệm của đa thức A(x) + B(x)
\(A(x)+B(x)=0\)
\(\Rightarrow \dfrac{{ – 1}}{4}(x + 1) = 0\)
Suy ra x = -1
Bài 3:
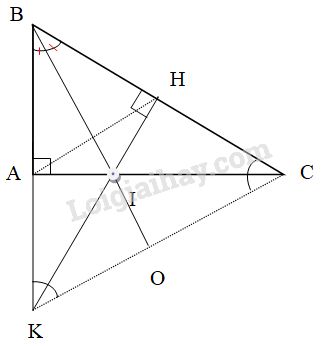
a) Tính BC ?
\(B{C^2} = A{B^2} + A{C^2} = 36 + 64 = 100\)
\(\Rightarrow BC = \sqrt {100} = 10cm\)
b) Chứng minh: \(\Delta ABI = \Delta HBI.\)
Xét hai tam giác vuông ABI và HBI có:
+) BI cạnh chung
+) \(\widehat {ABI} = \widehat {HBI}\) (Vì BI là phân giác)
Suy ra \(\Delta ABI = \Delta HBI.\) (cạnh huyền – góc nhọn)
c) Chứng minh: BI là đường trung trực của đoạn thẳng AH.
AB = AH vì (\(\Delta ABI = \Delta HBI\)) (1)
IA = IH vì (\(\Delta ABI = \Delta HBI\)) (2)
Từ (1) và (2), suy ra BI là đường trung trực của đoạn thẳng AH
d) Chứng minh: IA < IC
Ta có: AC > IH ( đường xiên – đường góc vuông )
IH = IA vì (\(\Delta ABI = \Delta HBI\))
Suy ra IA < IC
e) Chứng minh I là trực tâm \(\Delta ABC\)
Gọi O là giao điểm của BI và KC
Xét tam giác BKC có AC, HK là đường cao nên I là trực tâm của tam giác BKC






