Kiểm tra 45 phút 3 Chương 1 Đường thẳng vuông góc – đường thẳng song song môn Hình học 7: Px và PH có vuông góc với nhau không? Tại sao?

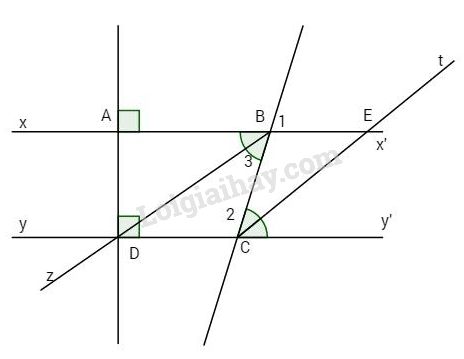
Bài 1. Cho hình vẽ, biết \( \Rightarrow AB//DE\) \(\widehat {{B_3}} = {80^o}\).

a) Tính số đo góc \(\widehat {{B_1}}\)và \(\widehat {{C_2}}\).

b) Vẽ tia phân giác Ct của \(\widehat {BCy’}\), tia Ct cắt xx’ ở E. So sánh \(\widehat {BCE}\) và \(\widehat {BEC}\).

c) Vẽ tia phân giác Bz của \(\widehat {ABC}\), vì sao Bz//EC?

Bài 2. Cho có \(\widehat A = {40^o}\). Trên tia đối của tia AC lấy điểm D. Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ tia Dx//BC. Biết \(\widehat {xDC} = {70^o}\).

a) Tính số đo góc \(\widehat {ACB}\).

b) Vẽ tia Ay là tia phân giác của \(\widehat {BAD}\). Chứng minh Ay // BC.

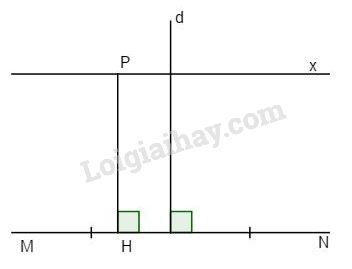
Bài 3. Cho đoạn thẳng MN. Từ một điểm P nằm ngoài đoạn thẳng Mn, vẽ PH vuông góc với MN (H thuộc MN) và Px//MN.

a) Px và PH có vuông góc với nhau không? Tại sao?

b) Vẽ trung trực d của đoạn NH, em có nhận xét gì về đường thẳng d và đường thẳng PH. Hãy giải thích nhận xét đó.

Bài 4. Cho hình vẽ.

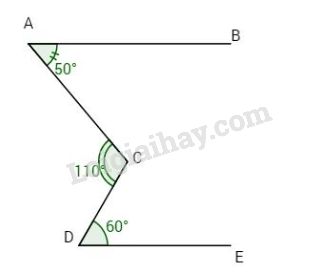
Chứng tỏ AB // DE.

Bài 1.

a) \(\widehat {{B_1}} = \widehat {{B_3}} = {80^o}\)(đối đỉnh)

Ta có \(\left\{ \matrix{xx’ \bot AD \hfill \cr yy’ \bot AD \hfill \cr} \right. \Rightarrow xx’//yy’\)

(hai đường thẳng phân biệt cùng vuông góc với đường thứ ba thì chúng song song với nhau)

\( \Rightarrow \widehat {{C_2}} + \widehat {{B_3}} = {180^o}\)(cặp góc trong cùng phía)

\( \Rightarrow \widehat {{C_2}} = {180^o} – \widehat {{B_3}} = {180^o} – {80^o} = {100^o}.\)

b) Ct là tia phân giác của góc \(\widehat {BCy’}\). Ta có \(\widehat {BCE} = \widehat {ECy’} = {1 \over 2}\widehat {BCy’}.\)

lại có xx’ // yy’\( \Rightarrow \widehat {BCE} = \widehat {ECy’}\)(cặp góc so le trong).

Do đó \(\widehat {BCE} = \widehat {BEC}.\)

Bài 2.

a) Dx // BC, hai góc \(\widehat {ACB}\) và \(\widehat {xDC}\) ở vị trí so le trong nên xx’//yy’ \( \Rightarrow \widehat {BCy’} = \widehat {ABC} \Rightarrow {{\widehat {BCy’}} \over 2} = {{\widehat {ABC}} \over 2}\) hay \(\widehat {zBC} = \widehat {BCE}\), hai góc này ở vị trí so le trong \( \Rightarrow Bz//CE.\)

\( \Rightarrow \widehat {ACB} = \widehat {xDC} = {70^o}.\)

b) Ta có \(\widehat {DAB} = {180^o} – \widehat {BAC} = {140^o}\)

Ay là phân giác của góc \(\widehat {DAB}\)

Nên \(\widehat {DAy} = \widehat {BAy} = {{\widehat {DAB}} \over 2} = {{{{140}^o}} \over 2} = {70^o}.\)

Hai góc \(\widehat {DAy}\) và \(\widehat {ACB}\) ở vị trí đồng vị, mà \(\widehat {DAy} = \widehat {ACB} = {70^o}.\)

Bài 3.

a) Ta có \(\left\{ \matrix{ PH \bot MN \hfill \cr Px//MN \hfill \cr}  \right. \Rightarrow Px \bot PH\) Do đó Ay // BC.

(một đường thẳng vuông góc với một trong hai đường song song thì nó vuông góc với đường còn lại).

b) d là trung trực của đoạn NH nên \(d \bot NH\), mà \(PH \bot NH \Rightarrow d//PH\)(hai đường thẳng phân biệt cùng vuông góc với đường thứ ba thì chúng song song).

Bài 4. Kẻ qua C tia Ct // AB (1) (tia Ct nằm trong góc \(\widehat {ACD}\), ta có \(\widehat {ACt} = \widehat {BAC} = {50^o}\)(cặp góc so le trong).

Tia Ct nằm giữa hai tia CD và CA, ta có \(\widehat {ACt} + \widehat {DCt} = \widehat {ACD}\)

\(\widehat {DCt} = \widehat {ACD} – \widehat {ACt} = {110^o} – {50^o} = {60^o}\). Hai góc \(\widehat {tDC}\) và \(\widehat {DCE}\) ở vị trí so le trong, mà \(\widehat {DCt} = \widehat {CDE} = {60^o}\) nên Ct // DE (2).

Từ (1) và (2) \( \Rightarrow AB//DE\) (hai đường thẳng phân bietj cùng song song với đường thẳng thứ ba).