Quan hệ giữa góc và cạnh đối diện trong tam giác: Giải bài 1,2 trang 55; Bài 3, 4, 5, 6, 7 trang 56 SGK Toán 7 tập 2 – Chương 3 Hình học 7.
Bài 1. So sánh các ∠ trong ΔABC, biết rằng:
AB = 2cm, BC = 4cm, AC = 5cm
Lời giải: Trong ΔABC có:
AB = 2cm ; BC = 4cm ; AC = 5cm
⇒ AB < BC < CA nên ∠C < ∠A < ∠B
Bài 2. So sánh các cạnh của ΔABC, biết rằng:
∠A = 800 , ∠B = 450
Lời giải:
ΔABC có ∠A = 800 , ∠B = 450
nên ∠C = 1800 – (800 + 450) = 550 (theo định lý tổng ba ∠ trong tam giác)
Vì 450 < 550 < 800 hay ∠B < ∠C < ∠A < ∠C ⇒ AC < AB < BC
Bài 3 trang 56. Cho ΔABC với ∠A = 1000, ∠B = 400
a) Tìm cạnh lớn nhất của Δ.
b) ΔABC là Δ gì?
a) ΔABC có ∠A = 1000 , ∠B = 400
Advertisements (Quảng cáo)
Cạnh lớn nhất của ΔABC là BC vì BC đối diện với ∠A và ∠A = 1000 > 900 nên ∠A là tù.
b) Trong ΔABC có:
∠A + ∠B + ∠C =1800 (Định lý tổng ba ∠ của một Δ)
Biết ∠A = 1000; ∠B = 400 (GT)
Thay số ta có : 1000 + 400 + ∠C = 1800 ⇒ ∠C = 400
Vậy ∠B = ∠C = 400
⇒ ΔABC là Δcân tại A.
Bài 4. Trong một Δ, đối diện với cạnh nhỏ nhất là góc gì ( nhọn, vuông, tù)? Tại sao?
Trong một Δ, đối diện với cạnh nhỏ nhất là ∠nhọn vì nếu ∠ đó là ∠vuông hoặc tù thì hai ∠ còn lại phải lớn hơn ∠vuông nên tổng ba ∠ của Δ lớn hơn 1800 ( vô lý với định lý tổng ba ∠ của Δ)
Advertisements (Quảng cáo)
Bài 5. Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường AD, BD, và CD (hình dưới). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng và ∠ACD là ∠tù. Hỏi ai đi xa nhất, ai đi gần nhất? Hãy giải thích
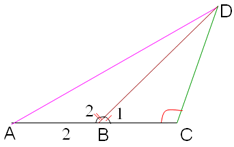
Trong ΔDBC có ∠C là ∠tù (gt) ⇒ DB > DC (1) và có ∠B1 nhọn.
Ta có ∠B1 + ∠B2 = 1800 (kề bù)
mà ∠B1 <900 (cmt) ⇒ ∠B2 > 900
Trong ΔDAB có ∠B2 là ∠tù (cmt) ⇒ DA > DB (2)
Từ (1) và (2) ta có DA > DB > DC
Vậy bạn Hạnh đi xa nhất; bạn Trang đi gần nhất.
Bài 6 trang 56 . Xem hình bên, có hai đoạn bằng nhau BC và DC. Hỏi rằng kết luận nào trong các kết luận sau là đúng? Tại sao?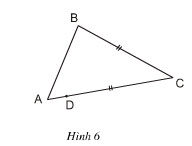
a) ∠A = ∠B
b) ∠A > ∠B
c) ∠A < ∠B
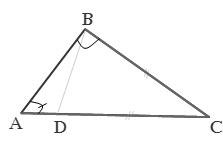
Ta có D nằm giữa A và C (gt) ⇒ AD + Dc = AC
mà DC = BC (gt) nên AD + BC = AC
Do đó BC < AC
Trong ΔABC ⇒ ∠A < ∠B (Quan hệ giữa góc và cạnh đối diện trong Δ)
Vậy kết luận c) là đúng.
Bài 7 trang 56 Toán 7. Cho ΔABC với AC > AB. Trên tia AC, lấy điểm B’ sao cho AB’ = AB
a) Hãy so sánh ∠ABC với ∠ABB’
b) Hãy so sánh ∠ABB’với ∠AB’B
c) Hãy so sánh ∠ABB’ với ∠ACB
Từ đó suy ra ∠ABC > ∠ACB
Lời giải: a) Vì AC > AB nên B’ nằm giữa A và C , do đó :
∠ABC > ∠ABB’ (1)
b) ΔABB’ có AB = AB’ nên ΔABB’ là một Δcân
Suy ra : ∠ABB’ = ∠AB’B (2 )
c) ∠AB’B là một góc ngoài tại đỉnh B’ của BB’C nên : ∠AB’B >∠ACB
Tư (1) và (2 ) ∠ABC > ∠ACB
