
I.TRẮC NGHIỆM (2đ)
Bài 1. Đánh dấu”x” thích hợp vào ô trống.
|
STT |
Khẳng định |
Đ |
S |
|
1 |
Hình tạo thành bởi ba đoạn thẳng AB, BC, AC gọi là tam giác ABC. |
|
|
|
2 |
Nếu AM = 5cm thì M nằm trên đường tròn (A ; 5cm). |
|
|
|
3 |
Nếu \(\widehat {xOy} = \widehat {yOz} = {1 \over 2}\widehat {xOz}\)thì tia Oy là tia phân giác của \(\widehat {xOz}\). |
|
|
|
4 |
Nếu \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)thì tia Ox nằm giữa Oy và tia Oz. |
|
|
Bài 2. Chọn chỉ một chữ cái đứng trước câu trả lời đúng.
1. Cho hai góc kề bù \(\widehat {AOB}\) và \(\widehat {BOC}\), biết \(\widehat {AOB} = 2.\widehat {BOC}\). Số đo \(\widehat {BOC}\)bằng
A.120o ; B.60o ; C. 90o ; D. 45o.
2. Cho hình vẽ 1, số góc có trong hình 1 là
A.6 ; B. 4 ;
C. 8 ; D. 5.
3. Cho 4 điểm, trong đó không có ba điểm nào thẳng hàng.
Số tam giác có đỉnh là ba trong bốn điểm trên là
Advertisements (Quảng cáo)
A.2 ; B. 6 ;
C. 8 ; D. 4.
4. Cho hình vẽ 2, tia MR nừm giữa hai tia
A.MN và MQ ;
B. MN và MQ ;
C. MP và MQ ;
Advertisements (Quảng cáo)
D. PM và NM.
II. TỰ LUẬN
Trên cùng một nửa mặt phẳng chứa tia Ox, vẽ hai tia Oy, Ot sao cho \(\widehat {xOy} = {30^o}\), \(\widehat {xOt} = {70^o}.\)
1) Tính \(\widehat {yOt}\).
2) Tia Oy có là tia phân giác của\(\widehat {xOt}\) không ? Vì sao ?
3) Gọi Om là tia đối của tia Ox. Tính số đo \(\widehat {mOt}\).
4) Gọi tia Oa là tia phân giác của \(\widehat {mOt}\). Tính số đo \(\widehat {aOx}\).

I.TRẮC NGHIỆM : 2 điểm (mỗi đáp án đúng 0,25đ)
Bài 1.
|
Câu |
1 |
2 |
3 |
4 |
|
Đáp án |
S |
Đ |
Đ |
S |
Bài 2.
|
Câu |
1 |
2 |
3 |
4 |
|
Đáp án |
B |
A |
D |
B |
II. TỰ LUẬN : Vẽ hình 0,5 điểm.
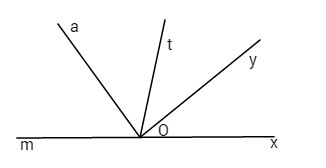
|
1 |
C/m tia Oy nằm giữa tia Ox và tia Ot. Dùng công thức cộng góc tính được \(\widehat {yOt} = {40^o}\) |
1,5đ |
|
2 |
Giải thích tia Oy không là tia phân giác của góc xOt. |
1,0đ |
|
3 |
Chỉ ra được hai góc kề bù. Tính được \(\widehat {mOt} = {110^o}\) |
2,5đ |
|
4 |
Tính được \(\widehat {xOa} = {125^o}\) |
2,5đ |



![[THCS Phạm Tuấn] thi học kì 2 môn Lý lớp 8 năm 2020: Tại sao xoong nồi thường làm bằng kim loại còn ấm, chén, bát đĩa lại thường làm bằng sứ?](https://dethikiemtra.com/wp-content/uploads/2020/07/82208322_457565911818124_3698770116704468992_n-100x75.jpg)


