A. PHẦN CÂU HỎI TRẮC NGHIỆM (5,0 đ)
1. : Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có \(A\left( {1; – 5} \right);\,\,B\left( {3;0} \right);\,\,C\left( { – 3;4} \right)\). Gọi M, N lần lượt là trung điểm của AB, AC. Tìm tọa độ vectơ \(\overrightarrow {MN} \) .
A. \(\overrightarrow {MN} = \left( { – 3;2} \right)\)
B. \(\overrightarrow {MN} = \left( {3; – 2} \right)\)
C. \(\overrightarrow {MN} = \left( { – 6;4} \right)\)
D. \(\overrightarrow {MN} = \left( {1;0} \right)\)
2. : Mệnh đề phủ định của mệnh đề “2018 là số tự nhiên chẵn” là
A. 2018 là số chẵn
B. 2018 là số nguyên tố.
C. 2018 không là số tự nhiên chẵn
D. 2018 là số chính phương
3. : Trục đối xứng của parabol \(y = 2{x^2} + 2x – 1\) là đường thẳng có phương trình:
A. \(x = 1\)
B. \(x = \frac{1}{2}\)
C. \(x = 2\)
D. \(x = – \frac{1}{2}\)
4. : Cho hai tập hợp \(A = \left( { – 3;3} \right)\) và \(B = \left( {0; + \infty } \right)\). Tìm \(A \cup B\).
A. \(A \cup B = \left( { – 3; + \infty } \right)\)
B. \(A \cup B = \left[ { – 3; + \infty } \right)\)
C. \(A \cup B = \left[ { – 3;0} \right]\)
D. \(A \cup B = \left( {0;3} \right)\)
5. : Cho tam giác ABC có G là trọng tâm. Mệnh đề nào sau đây sai?
A. \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với mọi điểm M
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
C. \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GA} \)
D. \(3\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {AC} \)
6. : Trong mặt phẳng Oxy cho \(A\left( {2; – 3} \right);\,\,B\left( {3;4} \right)\). Tọa độ điểm M nằm trên trục hoành sao cho ba điểm A, B, M thẳng hàng là:
A. \(M\left( {1;0} \right)\)
B. \(M\left( {4;0} \right)\)
C. \(M\left( { – \frac{5}{3}; – \frac{1}{3}} \right)\)
D. \(M\left( {\frac{{17}}{7};0} \right)\)
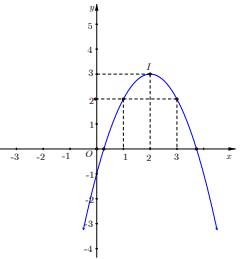
7. : Cho parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có đồ thị như hình bên. Tìm các giá trị của m để phương trình \(\left| {a{x^2} + bx + c} \right| = m\) có 4 nghiệm phân biệt.
A. \( – 1 < m < 3\)
B. \(0 < m < 3\)
C. \(0 \le m \le 3\)
D. \( – 1 \le m \le 3\)
8. : Tìm điều kiện của tham số m để hàm số \(y = \left( {3m + 4} \right)x + 5m\) đồng biến trên R.
A. \(m < – \frac{4}{3}\)
B. \(m > \frac{{ – 4}}{3}\)
C. \(m \ne – \frac{4}{3}\)
D. \(m = – \frac{4}{3}\)
9. : Tọa độ đỉnh I của parabol \(y = {x^2} – 2x + 7\) là:
A. \(I\left( { – 1; – 4} \right)\) B. \(I\left( {1;6} \right)\)
C. \(I\left( {1; – 4} \right)\) D. \(I\left( { – 1;6} \right)\)
1.0 : Mệnh đề phủ định của mệnh đề \(”\exists x \in R;\,\,{x^2} + x + 13 = 0”\) là :
A. \(”\forall x \in R;\,\,{x^2} + x + 13 \ne 0”\)
B. \(”\exists x \in R;\,\,{x^2} + x + 13 > 0”\)
C. \(”\forall x \in R;\,\,{x^2} + x + 13 = 0”\)
D. \(”\exists x \in R;\,\,{x^2} + x + 13 \ne 0”\)
1.1 : Trong mặt phẳng Oxy, cho tam giac MNP có \(M\left( {1; – 1} \right);\,\,N\left( {5; – 3} \right)\) và P thuộc trục Oy trọng tâm G của tam giác MNP nằm trên trục Ox. Tọa độ điểm P là:
Advertisements (Quảng cáo)
A. \(\left( {2;4} \right)\) B. \(\left( {0;4} \right)\)
C. \(\left( {0;2} \right)\) D. \(\left( {2;0} \right)\)
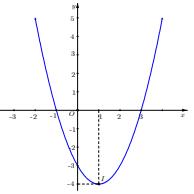
1.2 : Cho parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có đồ thị như hình bên. Khi đó \(2a + b + 2c\) có giá trị là:
A. \( – 9\) B. 9
C. \( – 6\) D. 6
1.3 : Cho hàm số \(f\left( x \right) = \left| {2x + 1} \right| + \left| {2x – 1} \right|\) và \(g\left( x \right) = 2{x^3} + 3x\). Khi đó khẳng định nào dưới đây là đúng?
A. \(f\left( x \right)\) là hàm lẻ và \(g\left( x \right)\) là hàm chẵn
B. \(f\left( x \right)\) và \(g\left( x \right)\) đều là hàm lẻ.
C. \(f\left( x \right)\) và \(g\left( x \right)\) đều là hàm chẵn
D. \(f\left( x \right)\) là hàm chẵn và \(g\left( x \right)\) là hàm lẻ.
1.4 : Tọa độ giao điểm của đường thẳng \(d:\,\,y = – x + 4\) và parabol \(y = {x^2} – 7x + 12\) là:
A. \(\left( { – 2;6} \right)\) và \(\left( { – 4;8} \right)\)
B. \(\left( {2;2} \right)\) và \(\left( {4;8} \right)\)
C. \(\left( {2; – 2} \right)\) và \(\left( {4;0} \right)\)
D. \(\left( {2;2} \right)\) và \(\left( {4;0} \right)\)
1.5 : Tìm tất cả các giá trị của m để đường thẳng \(y = mx + 3 – 2m\) cắt parabol \(y = {x^2} – 3x – 5\) tại 2 điểm phân biệt có hoành độ trái dấu.
A. \(m < – 3\)
B. \( – 3 < m < 4\)
C. m < 4.
D. \(m \le 4\)
1.6 : Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(6\sqrt 2 \) là số hữu tỷ.
B. Phương trình \({x^2} + 7x – 2 = 0\) có 2 nghiệm trái dấu.
C. 17 là số chẵn
D. Phương trình \({x^2} + x + 7 = 0\) có nghiệm.
Câu 17 : Cho hai tập hợp \(A = \left[ { – 2;3} \right]\) và \(B = \left( {1; + \infty } \right)\). Tìm \(A \cap B\).
A.\(A \cap B = \left[ { – 2; + \infty } \right)\)
B. \(A \cap B = \left( {1;3} \right]\)
C. \(A \cap B = \left[ {1;3} \right]\)
D. \(A \cap B = \left( {1;3} \right)\)
Câu 18 : Tập xác định của hàm số \(y = \sqrt {1 + 2x} + \sqrt {6 + x} \) là:
A. \(\left[ { – 6; – \frac{1}{2}} \right]\)
B. \(\left( { – \frac{1}{2}; + \infty } \right)\)
Advertisements (Quảng cáo)
C. \(\left[ { – \frac{1}{2}; + \infty } \right)\)
D. \(\left[ { – 6; + \infty } \right)\)
Câu 19 : Cho tập hợp \(A = \left( { – \infty ;2} \right]\) và \(B = \left( {0; + \infty } \right)\). Tìm \(A\backslash B\).
A. \(A\backslash B = \left( { – \infty ;0} \right]\)
B. \(A\backslash B = \left( {2; + \infty } \right)\)
C. \(A\backslash B = \left( {0;2} \right]\)
D. \(A\backslash B = \left( { – \infty ;0} \right)\)
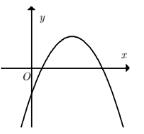
2.0 : Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. \(a < 0;\,\,b > 0;\,\,c > 0\).
B. \(a > 0;\,\,b < 0;\,\,c > 0\)
C. \(a < 0\,\,;b > 0;\,\,c < 0\)
D. \(a > 0;\,\,b > 0;\,\,c < 0\)
2.1 : Trong mặt phẳng Oxy, cho \(A\left( {{x_1};{y_1}} \right);\,\,B\left( {{x_2};{y_2}} \right)\). Tọa độ trung điểm của đoạn thẳng AB là:
A. \(I\left( {\frac{{{x_1} + {y_1}}}{2};\frac{{{x_2} + {y_2}}}{2}} \right)\)
B. \(I\left( {\frac{{{x_1} + {x_2}}}{3};\frac{{{y_1} + {y_2}}}{3}} \right)\)
C. \(I\left( {\frac{{{x_2} – {x_1}}}{2};\frac{{{y_2} – {y_1}}}{2}} \right)\)
D. \(I\left( {\frac{{{x_1} + {x_2}}}{2};\frac{{{y_1} + {y_2}}}{2}} \right)\)
Câu 22 : Trong mặt phẳng Oxy cho \(A\left( {2;4} \right);\,\,B\left( {4; – 1} \right)\) . Khi đó tạo độ của \(\overrightarrow {AB} \) là:
A. \(\overrightarrow {AB} = \left( { – 2;5} \right)\)
B. \(\overrightarrow {AB} = \left( {6;3} \right)\)
C. \(\overrightarrow {AB} = \left( {2;5} \right)\)
D. \(\overrightarrow {AB} = \left( {2; – 5} \right)\)
2.3 : Cho \(\overrightarrow a = \left( {2;1} \right);\,\,\overrightarrow b = \left( { – 3;4} \right);\,\,\overrightarrow c = \left( { – 4;9} \right)\). Hai số thực m,n thỏa mãn \(m\overrightarrow a + n\overrightarrow b = \overrightarrow c \). Tính \({m^2} + {n^2}\).
A. 5 B. 3
C. 4 D. 1
2.4 : Cho \(A = \left\{ {x \in R|\left| {mx – 3} \right| = mx – 3} \right\};\) \(B = \left\{ {x \in R|{x^2} – 4 = 0} \right\}\). Tìm m để \(B\backslash A = B\).
A. \( – \frac{3}{2} \le m \le \frac{3}{2}\)
B. \(m < \frac{3}{2}\)
C. \( – \frac{3}{2} < m < \frac{3}{2}\)
D. \(m \ge \frac{{ – 3}}{2}\)
2.5 : Trong mặt phẳng tọa độ Oxy cho tam giác ABC có \(M\left( { – \frac{5}{2}; – 1} \right);\,\,N\left( { – \frac{3}{2}; – \frac{7}{2}} \right);\,\,P\left( {0;\frac{1}{2}} \right)\) lần lượt là trung điểm các cạnh BC, CA, AB. Tìm trọng tâm G của tam giác ABC?
A. \(G\left( { – \frac{4}{3}; – \frac{4}{3}} \right)\) B. \(G\left( { – 4; – 4} \right)\)
C. \(G\left( {\frac{4}{3}; – \frac{4}{3}} \right)\) D. \(G\left( {4; – 4} \right)\)
B. PHẦN CÂU HỎI TỰ LUẬN (5,0 đ)
Câu I : (2,5đ)
1) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} – 4x + 3\)
2) Giải phương trình \(\sqrt {2{x^2} + 4x – 1} = x + 1\)
Câu II (1,5đ)
Trong hệ trục tọa độ Oxy cho bốn điểm \(A\left( {1;1} \right);\,\,B\left( {2; – 1} \right);\,\,C\left( {4;3} \right);\,\,D\left( {16;3} \right)\). Hãy phân tích vectơ \(AD\) theo hai vectơ \(\overrightarrow {AB} ;\,\,\overrightarrow {AC} \).
Câu III : Cho x, y là hai số thực thỏa mãn \(x + y \ge 2.\) Tìm giá trị nhỏ nhất của biểu thức \(P = 3\left( {{x^4} + {y^4} + {x^2}{y^2}} \right) – 2\left( {{x^2} + {y^2}} \right) + 1\) .

A. PHẦN CÂU HỎI TRẮC NGHIỆM (5,0 đ)
|
1. A |
2. C |
3. D |
4. A |
5. C |
|
6. D |
7. B |
8. B |
9. B |
10. A |
|
11. B |
12. C |
13. D |
14. D |
15. C |
|
16. B |
17. B |
18. C |
19. A |
20. C |
|
21. D |
22. D |
23. A |
24. C |
25. A |
B. PHẦN CÂU HỎI TỰ LUẬN (5,0 đ)
Câu I: 1) +) TXĐ: \(D = R\)
+) Đỉnh \(I\left( {2; – 1} \right)\), trục đối xứng \(x = 2\)
+) Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { – \infty ;2} \right)\).
BBT:
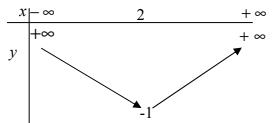
+) Đồ thị:
Giao với Ox: \(y = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
Giao với Oy: \(x = 0 \Leftrightarrow y = 3\)
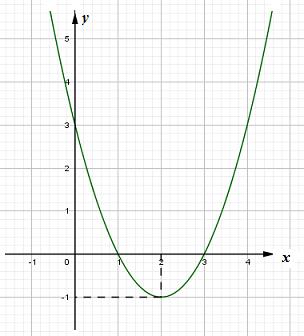
2) \(\sqrt {2{x^2} + 4x – 1} = x + 1\)
\(\Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\2{x^2} + 4x – 1 = {\left( {x + 1} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\2{x^2} + 4x – 1 = {x^2} + 2x + 1\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\{x^2} + 2x – 2 = 0\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x \ge – 1\\\left[ \begin{array}{l}x = – 1 + \sqrt 3 \,\,\left( {tm} \right)\\x = – 1 – \sqrt 3 \,\,\left( {ktm} \right)\end{array} \right.\end{array} \right.\)
\(\Leftrightarrow x = – 1 + \sqrt 3 \)
Vậy nghiệm của phương trình là \(x = – 1 + \sqrt 3 \).
Câu II: Ta có: \(\overrightarrow {AD} = \left( {15;2} \right);\)\(\,\,\overrightarrow {AB} = \left( {1; – 2} \right);\,\,\overrightarrow {AC} = \left( {3;2} \right)\)
Giả sử tồn tại các số thực m,n sao cho \(\overrightarrow {AD} = m\overrightarrow {AB} + n\overrightarrow {AC} \) ta có:
\(\left\{ \begin{array}{l}15 = m + 3n\\2 = – 2m + 2n\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}m = 3\\n = 4\end{array} \right. \)
\(\Rightarrow \overrightarrow {AD} = 3\overrightarrow {AB} + 4\overrightarrow {AC} \).
Câu III: \(P = 3\left( {{x^4} + {y^4} + {x^2}{y^2}} \right) – 2\left( {{x^2} + {y^2}} \right) + 1\)
Ta tìm các hằng số \(m,n \in R\) sao cho \({x^4} + {y^4} + {x^2}{y^2} = m{\left( {{x^2} + {y^2}} \right)^2} + n{\left( {{x^2} – {y^2}} \right)^2}\)
Ta có :
\(\begin{array}{l}\,\,\,m{\left( {{x^2} + {y^2}} \right)^2} + n{\left( {{x^2} – {y^2}} \right)^2}\\ = m\left( {{x^4} + {y^4} + 2{x^2}{y^2}} \right) + n\left( {{x^4} + {y^4} – 2{x^2}{y^2}} \right)\\ = \left( {m + n} \right)\left( {{x^4} + {y^4}} \right) + \left( {2m – 2n} \right){x^2}{y^2}\end{array}\)
Đồng nhất hệ số ta được \(\left\{ \begin{array}{l}m + n = 1\\2\left( {m – n} \right) = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{3}{4}\\n = \dfrac{1}{4}\end{array} \right.\)
\( \Rightarrow {x^4} + {y^4} + {x^2}{y^2} = \dfrac{3}{4}{\left( {{x^2} + {y^2}} \right)^2} + \dfrac{1}{4}{\left( {{x^2} – {y^2}} \right)^2} \ge \dfrac{3}{4}{\left( {{x^2} + {y^2}} \right)^2}\)
\(\begin{array}{l}P = 3\left( {{x^4} + {y^4} + {x^2}{y^2}} \right) – 2\left( {{x^2} + {y^2}} \right) + 1 \ge 3.\dfrac{3}{4}{\left( {{x^2} + {y^2}} \right)^2} – 2\left( {{x^2} + {y^2}} \right) + 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{9}{4}{\left( {{x^2} + {y^2}} \right)^2} – 2\left( {{x^2} + {y^2}} \right) + 1\end{array}\)
Đặt \(t = {x^2} + {y^2}\) ta có \({x^2} + {y^2} – 2xy \ge 0 \)
\(\Leftrightarrow 2\left( {{x^2} + {y^2}} \right) \ge {x^2} + {y^2} + 2xy\)
\(\Leftrightarrow {x^2} + {y^2} \ge \dfrac{1}{2}{\left( {x + y} \right)^2}\)
\( \Leftrightarrow t = {x^2} + {y^2} \ge \dfrac{1}{2}{.2^2} = 2\)
Khi đó \(P \ge \dfrac{9}{4}{t^2} – 2t + 1\)
Xét hàm số \(f\left( t \right) = \dfrac{9}{4}{t^2} – 2t + 1\) với \(t \ge 2\) ta có BBT :
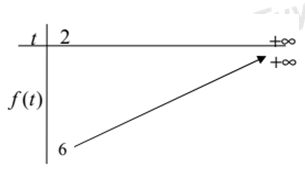
Từ BBT ta có \(f\left( t \right) \ge 6 \Rightarrow P \ge 6\).
Dấu “=” xảy ra \( \Leftrightarrow t = 2\)
\(\Leftrightarrow \left[ \begin{array}{l}{x^2} + {y^2} = 2\\x + y = 2\end{array} \right.\)
\(\Leftrightarrow \left\{ {x = y = 1} \right.\).
Vậy \(\min P = 6 \Leftrightarrow x = y = 1\).