Đề kiểm tra 15 phút môn Toán Chương 2 Hình học 8: Chứng minh rằng: S(ABCD) = 1/2( BD.CH + AE. IH)

Ngũ giác ABCDE có các đỉnh lần lượt theo thứ tự đó. Có các điều kiện sau: \(BD// AE;CH \bot AE\left( {H \in AE} \right).\) Gọi I là giao điểm của BD và CH.

Chứng minh rằng: \({S_{ABCDE}} = \dfrac{1}{ 2}\left( {BD.CH + AE.IH} \right).\)

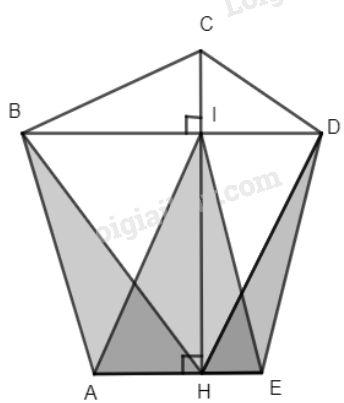
Ta có: \({S_{ABCDE}} = {S_{BCDH}} + {S_{ABH}} + {S_{EDH}}\)

Mà \({S_{ABH}} = {S_{AHI}}\) (cùng chung đáy AH và hai đường cao bằng nhau)

Tương tự: \({S_{EDH}} = {S_{EIH}}.\)

Cộng vế với vế của hai đẳng thức trên:

\( \Rightarrow {S_{ABH}} + {S_{EDH}} = {S_{AIH}} + {S_{EIH}}\)

                           \( = {S_{AIE}} = \dfrac{1 }{2}AE.IH\)

Lại có \({S_{BCDH}} = \dfrac{1 }{ 2}BD.CH\)

(tứ giác BCDH có hai đường chéo vuông góc)