
Bài 1: Cho điểm M nằm ngoài đường tròn (O; R). Vẽ tiếp tuyến MA ( A là tiếpđ), cát tuyến MBC ( B nằm giữa M và C) và O nằm trong góc AMC. Lấy I là trung điểm của BC. Tia OI cắt cung nhỏ BC tại N, AN cắt BC tại D.
a) Chứng minh AD là phân giác của góc BAC.
b) Chứng minh : MD2 = MB.MC.
c) Gọi H, K là hình chiếu của N lên AB và AC. Chứng tỏ ba điểm H, I, K thẳng hàng ( đường thẳng Sim-Sơn).
Bài 2: Cho đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại A. Qua A vẽ đường thẳng cắt (O) tại B và cắt (O’) tại C.
a) Chứng tỏ OB // O’C.
b) Chứng tỏ tỉ số diện tích hai hình quạt nằm trong góc ở tâm \(\widehat {AOB}\) và \(\widehat {AO’C}\) của hai hình tròn không đổi khi cát tuyến BAC quạt quanh A.

Bài 1:
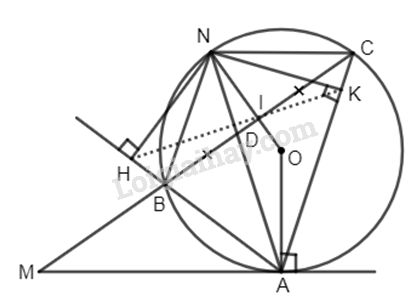
a) I là trung điểm BC \(\Rightarrow OI \bot BC \Rightarrow \overparen{ NB} = \overparen{ NC}\)
Do đó \(\widehat {BAN} = \widehat {CAN}\) hay AD là phân giác của góc \(\widehat {BAC}\).
Advertisements (Quảng cáo)
b) Xét ∆MAB và ∆MCA có:
+) \(\widehat M\) chung,
+) \(\widehat {MAB} = \widehat {MCA}\) (góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung AB)
Do đó ∆MAB và ∆MCA đồng dạng (g.g)
\( \Rightarrow \dfrac{{MA}}{ {MC}} = \dfrac{{MB} }{{MA}}\)
\( \Rightarrow MA^2= MB.MC\) (1)
Lại có \(\widehat {MDA} = \dfrac{{sđ\overparen{AB} +sđ\overparen{ NC}}}{2}\) ( góc có đỉnh bên trong đường tròn)
Advertisements (Quảng cáo)
\(\widehat {MAN} = \dfrac{{sđ\overparen{AB} + sđ\overparen{BN}}}{2}\) ( góc giữa tiếp tuyến và một dây)
Mà \(\overparen{ NC} = \overparen{ NB} \)\(\,\Rightarrow \widehat {MDA} = \widehat {MAN}\) hay ∆MAD cân tại M
\( \Rightarrow MA = MD\) (2)
Thay (2) vào (1), ta có : \(MD^2 = MB.MC.\)
c) Tứ giác HBIN nội tiếp ( \(\widehat {NHB} + \widehat {NIB} = 180^\circ ),\)
\(\widehat {HBN} = \widehat {HIN}\) (1) ( các góc nội tiếp cùng chắn cung HN)
mà \(\widehat {HBN} = \widehat {ACN}\) (2) ( cùng bù với \(\widehat {ABN}\))
Mặt khác tứ giác NIKC nội tiếp ( \(\widehat {NIC} = \widehat {NKC} = 90^\circ \))
\( \Rightarrow \widehat {ACN} + \widehat {NIK} = 180^\circ \) (3)
Từ (1), (2) và (3) \( \Rightarrow \widehat {HIN} + \widehat {NIK} = 180^\circ \) chứng tỏ ba điểm H, I, K thẳng hàng.
Bài 2:
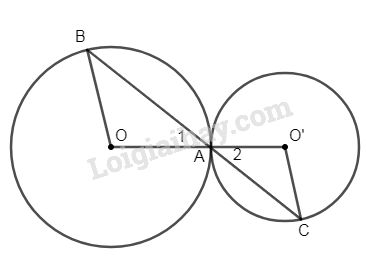
a) Ta có \(\widehat {{A_1}} = \widehat {{A_2}}\) ( đối đỉnh)
∆BOA cân \( \Rightarrow \widehat {{A_1}} = \widehat B\).
Tương tự \(\widehat {{A_2}} = \widehat C \Rightarrow \widehat B = \widehat C\)
Do đó OB // O’C ( cặp góc so le trong bằng nhau).
b) Ta có : \({S_{\overparen{AOB}}} = \dfrac{{\pi {R^2}n} }{ {360}}\)
\({S_{\overparen{AO’C}}} = \dfrac{{\pi R{‘^2}n} }{{360}}\)
\( \Rightarrow \dfrac{{{S_{\overparen{AOB}}}}}{{{S_{\overparen{AO’C}}}}} = \dfrac{{{R^2}} }{ {R{‘^2}}}\) ( không đổi).






