Cho tam giác ABC, trung tuyến AM. Vẽ đường thẳng d qua trung điểm I của AM, cắt các cạnh AB, AC. Gọi \(A’,B’,C’\) theo thứ tự là hình chiếu của A, B, C lên d … trong Đề kiểm tra 15 phút môn Toán Chương 1 Hình học 8. Xem Đề và đáp án đầy đủ phía dưới đây

Cho tam giác ABC, trung tuyến AM. Vẽ đường thẳng d qua trung điểm I của AM, cắt các cạnh AB, AC. Gọi \(A’,B’,C’\) theo thứ tự là hình chiếu của A, B, C lên d. Chứng minh: \(BB’ + CC’ = 2AA’.\)

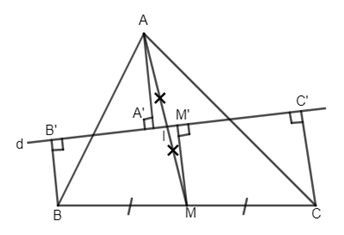
Ta có \(BB’ \bot d,CC’ \bot d \Rightarrow BB’//CC’\) nên \(BB’C’C\) là hình thang.
Advertisements (Quảng cáo)
M là trung điểm của BC (gt), \(MM’ \bot d \Rightarrow MM’// BB’// CC’\) nên \(MM’\) là đường trung bình của hình thang \(BB’C’C\) ta có:
\(MM’ = \dfrac{BB’ + CC’} { 2}\)
\(\Rightarrow BB’ + CC’ = 2MM’.\)
Advertisements (Quảng cáo)
Lại có \(\Delta AA’I = \Delta MM’I\) (cạnh huyền – góc nhọn) \( \Rightarrow AA’ = MM’.\)
Vậy \(BB’ + CC’ = 2AA’.\)






