Bài 1. Phân tích thành nhân tử:
a) \(9 – {x^2} + 6xy – 9{y^2}\)
b) \({x^4} – 2{x^2}.\)
Bài 2. Tìm m để \(P = {x^3} + 3{x^2} + mx + 8\) chia hết cho \(Q = x + 4.\)
Bài 3. Cho \({x \over y} = 10.\) Tính giá trị của biểu thức \(M = {{16{x^2} – 40xy} \over {8{x^2} – 24xy}}.\)
Bài 4. Cho biểu thức: \(A = {{5x – 6} \over {4 – {x^2}}} + {4 \over {x + 2}} + {2 \over {x – 2}}.\)
a) Tìm điều kiện xác định của biểu thức A.
b) Rút gọn biểu thức A.
Bài 5. Cho tam giác ABC cân tại A. Trên đường thẳng đi qua đỉnh A và song song với BC lấy hai điểm M và N sao cho A là trung điểm của MN (M, B cùng thuộc một nửa mặt phẳng bờ AC). Gọi H, I, K lần lượt là trung điểm của cạnh MB, BC và CN.
Chứng minh rằng tứ giác AHIK là hình thoi.
Bài 6. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi D là điểm đối xứng với A qua M và K là trung điểm của MC, E là điểm đối xứng của D qua K.
a) Chứng minh tứ giác ABDC là hình thoi.
b) Chứng minh tứ giác AMCE là hình chữ nhật.
c) AM và BE cắt nhau tại I. Chứng minh rằng I là trung điểm của BE.
d) Chứng minh rằng AK, CI, EM đồng quy.
Bài 1. a) \(9 – {x^2} + 6xy – 9{y^2} = 9 – \left( {{x^2} – 6xy + 9{y^2}} \right) = 9 – {\left( {x – 3y} \right)^2}\)
\( = \left( {3 – x + 3y} \right)\left( {3 + x – 3y} \right).\)
b)\({x^4} – 2{x^2} = {x^2}\left( {{x^2} – 2} \right) \)
Advertisements (Quảng cáo)
\(= {x^2}\left[ {{x^2} – {{\left( {\sqrt 2 } \right)}^2}} \right] \)
\(= {x^2}\left( {x + \sqrt 2 } \right)\left( {x – \sqrt 2 } \right).\)
Bài 2. \(\matrix{ – \hfill \cr {} \hfill \cr – \hfill \cr {} \hfill \cr – \hfill \cr {} \hfill \cr } \matrix{ {\,\,{x^3} + 3{x^2} + mx + 8} \hfill \cr {\underline {\,\,{x^3} + 4{x^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} } \hfill \cr {\,\,\,\,\,\,\,\, – {x^2} + mx + 8} \hfill \cr {\,\,\,\,\,\,\,\,\underline { – {x^2} – 4x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {m + 4} \right)x + 8} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline {\left( {m + 4} \right)x + 4m + 16\,\,} } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, – 4m – 8} \hfill \cr} \matrix{ {x + 4} \hfill \cr {{x^2} – x + m + 4} \hfill \cr {} \hfill \cr {} \hfill \cr {} \hfill \cr {} \hfill \cr {} \hfill \cr } \)
P chia hết cho Q khi và chỉ khi \( – 4m – 8 = 0 \Leftrightarrow m = – 2.\)
Bài 3. Ta có: \(M = {{8x\left( {2x – 5y} \right)} \over {8x\left( {x – 3y} \right)}}\)
Vì \({x \over y} = 10\left( {y \ne 0} \right) \Rightarrow x = 10y\left( {y \ne 0} \right)\)
Vậy \(M = {{2x – 5y} \over {x – 3y}}.\) Thế \(x = 10y,\) ta có: \(M = {{20y – 5y} \over {10y – 3y}} = {{15} \over 7}.\)
Bài 4. a) Điều kiện: \(x + 2 \ne 0\) và \(x – 2 \ne 0\) hay \(x \ne \pm 2\)
(Khi đó \({x^2} – 4 = \left( {x – 2} \right)\left( {x + 2} \right) \ne 0).\)
b)\(A = {{ – \left( {5x – 6} \right)} \over {{x^2} – 4}} + {4 \over {x + 2}} + {2 \over {x – 2}} = {{ – 5x + 6 + 4\left( {x – 2} \right) + 2\left( {x + 2} \right)} \over {{x^2} – 4}}\)
\( = {{ – 5x + 6 + 4x – 8 + 2x + 4} \over {{x^2} – 4}} = {{x + 2} \over {\left( {x – 2} \right)\left( {x + 2} \right)}} = {1 \over {x – 2}}.\)
Bài 5.
Advertisements (Quảng cáo)
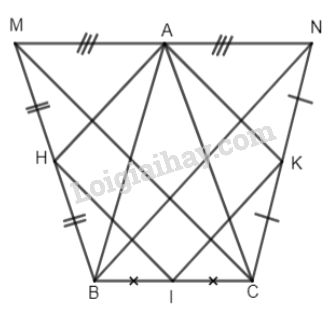
Ta có: \(MN\parallel BC\left( {gt} \right)\)
\( \Rightarrow \widehat {MAB} = \widehat {ABC}\) (so le trong)
Tương tự: \(\widehat {NAC} = \widehat {ACB}\)
mà \(\widehat {ABC} = \widehat {ACB}\) (gt)
Do đó \(\widehat {MAB} = \widehat {NAC}\)
Dễ thấy \(\Delta MAB = \Delta NAC\left( {c.g.c} \right)\)
\( \Rightarrow \widehat {BMA} = \widehat {CNA}\)
Vậy MNCB là hình thang cân.
Nối B với N, C với M ta có HA và KI lần lượt là các đường trung bình của \(\Delta MBN\) và \(\Delta NCB\) nên \(HA\parallel BN\) và \(HA = {1 \over 2}BN.\)
Tương tự \(IK\parallel BN\) và \(IK = {1 \over 2}BN.\) Do đó \(HA\parallel IK\) nên AHIK là hình bình hành.
Chứng minh tương tự ta có \(AK\parallel MC\) và \(AK = {1 \over 2}MC\) mà BN = MC (tính chất hai đường chéo của hình thang cân) \( \Rightarrow HA = KA.\)
Do đó AHIK là hình thoi.
Bài 6.
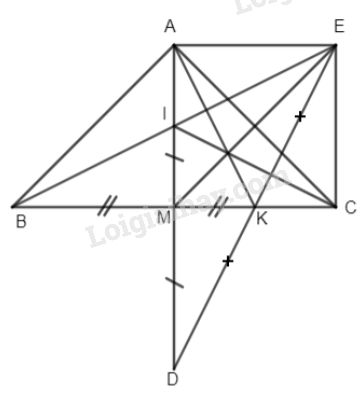
a) Ta có MB = MC (gt)
MD = MA (tính chất đối xứng) nên ABCD là hình bình hành.
Lại có AB = AC (gt)
\( \Rightarrow \) Tứ giác ABDC là hình thoi.
b)E đối xứng với D qua K nên K là trung điểm của DE, M là trung điểm của AD nên MK là đường trung bình của \(\Delta AED.\)
\( \Rightarrow MK\parallel AE\) và \(MK = {1 \over 2}AE.\)
Lại có K là trung điểm của MC (gt) \( \Rightarrow MC\parallel AE\) và MC = AE.
Do đó tứ giác AMCE là hình bình hành.
\(\Delta ABC\) cân có trung tuyến AM nên AM đồng thời là đường cao hay \(AM \bot BC \Rightarrow \widehat {AMC} = {90^ \circ }\) .
Vậy AMCE là hình chữ nhật.
c) Ta có \(AE\parallel MC\) và AE = MC (cmt)
\( \Rightarrow AE\parallel MB\) và AE = MB
nên tứ giác AEMB là hình bình hành và I là giao điểm hai đường chéo nên I là trung điểm của BE.
d) Ta có AMCE là hình chữ nhật (cmt) nên ME đi qua trung điểm của AC. Lại có I, K theo thứ tự là trung điểm của AM (cmt) và MC (gt).
Do đó AK, CI, EM là ba đường trung tuyến của \(\Delta AMC\) nên chúng đồng quy.
