
Bài 1. Thực hiện phép tính:
a) \({{{x^2} – x + 1} \over {{x^2} – 1}}:{{{x^3} + 1} \over {3x – 3}}\)
b) \({1 \over {x + 1}} + {1 \over {x – 1}} + {2 \over {1 – {x^2}}}.\)
Bài 2. Phân tích đa thức \(3a – 3b – {a^2} + 2ab – {b^2}\) thành nhân tử.
Bài 3. Cho biểu thức \(A = {{{x^4} – 4{x^3} + 4{x^2}} \over {{x^3} – 4x}}.\)
a) Rút gọn biểu thức A.
b) Tìm giá trị x để giá trị của biểu thức A bằng 0.
Bài 4. Tìm m để \(P = {x^4} – {x^3} + 6{x^2} – x + m\) chia hết cho \(Q = 2{x^2} – x + 5.\)
Bài 5. Cho tam giác ABC, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm F sao cho \(MF = MB.\) Gọi E là điểm đối xứng của F qua A và N là trung điểm của AB.
a) Chứng minh rằng E, N, C thẳng hàng.
b)\(\Delta ABC\) cân có điều kiện gì để EBCF là hình thang cân.
Bài 6. Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.
a) Gọi D là điểm đối xứng của A qua N. Chứng minh tứ giác ABDC là hình chữ nhật.
b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I. Chứng minh tứ giác ANCE là hình thoi.
c) Đường thẳng BC cắt DM và DI lần lượt tại G và \({G’}\). Chứng minh \(BG = C{G’}.\)
d) Cho AB = 6cm, AC = 8cm. Tính diện tích \(\Delta DG{G’}\).

Advertisements (Quảng cáo)
Bài 1.
a) Điều kiện: \(x \ne \pm 1\) .
\({{{x^2} – x + 1} \over {{x^2} – 1}}:{{{x^3} + 1} \over {3x – 3}} = {{{x^2} – x + 1} \over {\left( {x – 1} \right)\left( {x + 1} \right)}}.{{3\left( {x – 1} \right)} \over {\left( {x + 1} \right)\left( {{x^2} – x + 1} \right)}} = {3 \over {{{\left( {x + 1} \right)}^2}}}\)
b) Điều kiện: \(x \ne \pm 1.\)
\({1 \over {x + 1}} + {1 \over {x – 1}} + {2 \over {1 – {x^2}}} = {1 \over {x + 1}} + {1 \over {x – 1}} – {2 \over {{x^2} – 1}} = {{x – 1 + x + 1 – 2} \over {{x^2} – 1}}\)
\( = {{2x – 2} \over {{x^2} – 1}} = {{2\left( {x – 1} \right)} \over {\left( {x – 1} \right)\left( {x + 1} \right)}} = {2 \over {x + 1}}.\)
Bài 2. \(3a – 3b – {a^2} + 2ab – {b^2} = 3\left( {a – b} \right) – \left( {{a^2} – 2ab + {b^2}} \right) = 3\left( {a – b} \right) – {\left( {a – b} \right)^2}\)
\( = \left( {a – b} \right)\left( {3 – a + b} \right)\)
Bài 3. a) Điều kiện: \(x \ne 0;x \ne \pm 2.\)
\(A = {{{x^2}\left( {{x^2} – 4x + 4} \right)} \over {x\left( {{x^2} – 4} \right)}} = {{x{{\left( {x – 2} \right)}^2}} \over {\left( {x – 2} \right)\left( {x + 2} \right)}} = {{x\left( {x – 2} \right)} \over {x + 2}}.\)
b) Điều kiện: \(x \ne 0\) và \({x^2} – 4 \ne 0 \Rightarrow x \ne 0\) và \(x \ne \pm 2\)
Advertisements (Quảng cáo)
\(A = 0 \Rightarrow x\left( {x – 2} \right) = 0 \Rightarrow x = 0\) hoặc \(x – 2 = 0 \Rightarrow x = 0\) hoặc x = 2.
(không thỏa mãn các điều kiện \(x \ne 0\) và \(x \ne 2\))
Vậy không có giá trị x để A = 0.
Bài 4.
\({x^4} – {x^3} + 6{x^2} – x + m \)\(\,= \left( {{x^2} – x + 5} \right)\left( {{x^2} + 1} \right) + m – 5\)
P chia hết cho Q khi \(m – 5 = 0 \Rightarrow m = 5.\)
Bài 5.
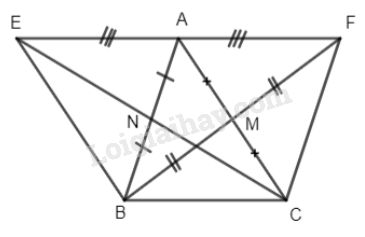
a) Ta có MA = MC (gt) ; MB = MF (gt)
Do đó AFCB là hình bình hành \( \Rightarrow AF\parallel BC\) và AF = BC.
Lại có E đối xứng với F qua A (gt) nên AE = AF.
\( \Rightarrow AE = BC\) và \(AE\parallel BC\) nên tứ giác ACBE là hình bình hành, mà N là trung điểm của đường chéo AB nên đường chéo thứ hai EC phải qua N. Hay E, N, C thẳng hàng.
b) Ta có \(BC\parallel {\rm{AF}}\) nên EBCF là hình thang.
Hình thang EBCF là hình thang cân \( \Leftrightarrow \widehat {BEF} = \widehat {CFE}\)
Mà \(\widehat {BEF} = \widehat {ACB},\widehat {CFE} = \widehat {ABC}\) (do ACBE và AFCB là các hình bình hành) \( \Leftrightarrow \widehat {ABC} = \widehat {ACB} \Leftrightarrow \Delta ABC\) cân tại A.
Bài 6.

a) Ta có: NB = NC (gt); ND = NA (gt) nên ABDC là hình hành có \(\widehat A = {90^ \circ }(gt) \Rightarrow ABDC\)là hình chữ nhật.
b) Chứng minh tương tự ta có AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
Mặt khác \(\Delta ABC\) vuông có AN là trung tuyến nên \(AN = NC = {1 \over 2}BC.\)
Vậy tứ giác AECN là hình thoi.
c) Dễ thấy G và \(G’\) là trọng tâm của hai tam giác ABD và ACD nên \(BG = {2 \over 3}BN\) và \(CG’ = {2 \over 3}CN\) mà \(BN = CN \Rightarrow BG = CG’.\)
d) Ta có: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.6.8 = 24\left( {c{m^2}} \right)\)
Lại có: \(BG = GG’ = CG’\) (tính chất trọng tâm)
\( \Rightarrow {S_{BGD}} = {S_{GG’D}} = {S_{G’CD}}\left( { = {1 \over 3}{S_{BCD}}} \right)\)
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà \({S_{BCD}} = {S_{CBA}}\) (vì \(\Delta BCD = \Delta CBA\left( {c.c.c} \right)\) )
\( \Rightarrow {S_{DGG’}} = {1 \over 3}{S_{CBA}} = {1 \over 3}.24 = 8\left( {c{m^2}} \right).\)


![[THCS Hiệp Phước] kiểm tra học kì 2 môn Sinh lớp 8: Nguy cơ có thai ở tuổi vị thành niên dẫn đến những hậu quả gì? Là học sinh các em có nhận thức gì về vấn đề này?](https://dethikiemtra.com/wp-content/uploads/2020/06/Tổng-hợp-những-hình-ảnh-đẹp-về-biển-4-100x75.jpg)
![[THCS Trần Cao] thi môn Toán lớp 8 cuối học kì 2: Mẫu số của một phân số lớn hơn tử số của nó là 5, nếu tăng cả tử lẫn mẫu của nó thêm 5 đơn vị thì được phân số mới bằng phân số 2 /3. Tìm phân số ban đầu](https://dethikiemtra.com/wp-content/uploads/2020/09/anh-chup-dep-ve-gia-dinh_035107328-100x75.jpg)

![[Phòng GD & ĐT Hà Tĩnh] thi cuối năm học lớp 8 môn Toán: ho tam giác ABC cân tại A và M là trung điểm của BC. Lấy các điểm D, E theo thứ tự thuộc các cạnh AB, AC sao cho góc DME = góc B. Chứng minh ΔBDM đồng dạng với Δ CME](https://dethikiemtra.com/wp-content/uploads/2020/09/anh_1_INQG-100x75.jpg)
