Mời các em cùng thử sức với tài liệu khá hay dưới đây: Đề thi học kì 1 lớp 8 môn Toán của Phòng GDĐT Thái Bình năm học 2016 – 2017.
Bài1. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
1. Rút gọn biểuthức (x2 – 5)(x + 3) + (x + 4)(x – x2) được kết quả là -(x + 15).
2. Với mọi số a ∈ Z thì a2 + 2a + 4 luôn là một số chính phương.
3. Hình thang có hai đường chéo bằng nhau là hình thang cân.
4. Hình chữ nhật có hai cạnh bằng 5m và 12m. Đường chéo của hình chữ nhật đó bằng 13m.
Bài2. 1. Tính giá trị của biểuthức P = y3 – 3y2 + 3y – 1 tại y = 201.
2. Phân tích đathức thành nhân tử
a) 5x2 – 5xy – 9x + 9y b) m3 + 4m2 + 3m
Bài3. 1. Tìm số thực k để đathức 3x3 + 2x2 – x + k chia hết cho đathức x – 1 ?
2. Chứng minh biểu thức Q = x2 – x + 3 luôn có giá trị dương với mọi giá trị của biến x.
Bài4.
Cho biểu thức : 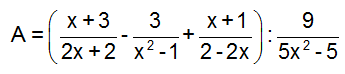
1. Tìm điều kiện của x để giá trị của biểu thức A được xác định ?
2. Chứng minh khi giá trị của biểu thức A được xác định thì giá trị đó không phụ thuộc vào giá trị của x.
Advertisements (Quảng cáo)
Bài5 Cho tứ giác ABCD. Gọi R, S, K, T thứ tự là trung điểm của AB, BC, CD, DA. Nối A với C, B với D.
1. Chứng minh tứ giác RSKT là hình bình hành.
2. Hai đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì RSKT là:
a) Hình thoi ?
b) Hình vuông ?
Bài6.
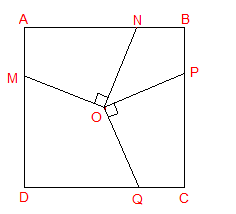
1. Cho hình vẽ bên: Hình vuông ABCD có tâm đối xứng O, cạnh 4cm. Hai tứ giác AMON và CPOQ có góc MON = góc POQ = 900 (M ∈ AD, N ∈ AB, P ∈ BC, Q ∈ CD). Người ta tô màu phần diện tích của hai tứ giác MOQD và NOP
B.Tính diện tích phần được tô màu ?
2. Cho x, y, z là ba số thực khác 0 thỏa mãn đồng thời: x + y + z = a và 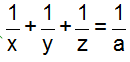
Tính giá trị biểu thức S = (x5 – a5)(y7 – a7)(z9 – a9).
Advertisements (Quảng cáo)
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
Bài1:
|
1 |
2 | 3 |
4 |
|
Đúng |
Sai | Đúng |
Đúng |
Bài2:
1. P = y3 – 3y2 + 3y – 1 = (y – 1)3
Thay y = 201 vào biểu thức P ta có:
P = (201 – 1)3 = 2003 = 8000000
Vậy P = 8000000 tại y = 201.
2. a) 5x2 – 5xy – 9x + 9y = (5x2 – 5xy) – (9x – 9y)
= 5x(x – y) – 9(x – y)
= (x – y)(5x – 9)
b) m3 + 4m2 + 3m = m(m2 + 4m + 3)
= m(m2 + m + 3m + 3)
= m[m(m + 1) + 3(m + 1)]
= m(m + 1)(m + 3)
Bài3. Thực hiện phép chia đathức 3x3 + 2x2 – x + k cho đathức x – 1 được thương là 3x2 + 5x + 4 và dư là k + 4.
3x3 + 2x2 – x + k chia hết cho x – 1 khi k + 4 = 0 hay k = -4.
Vậy k = -4 thì 3x3 + 2x2 – x + k chia hết cho x – 1.
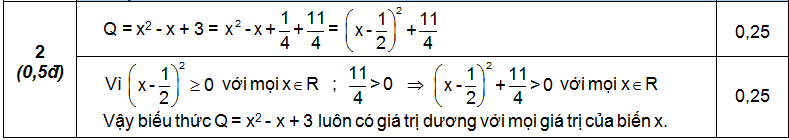
Bài4
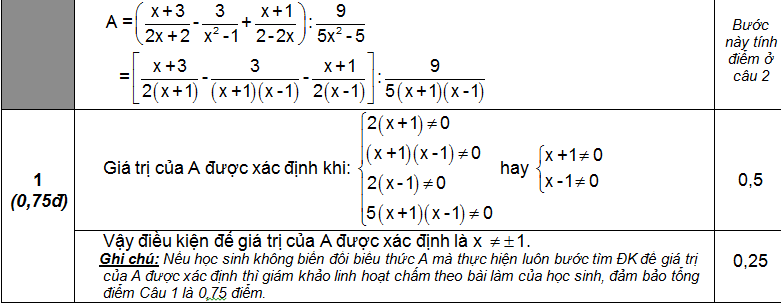

Bài5