Tìm tập hợp (quỹ tích) các điểm cách đều hai đường thẳng song song cho trước.

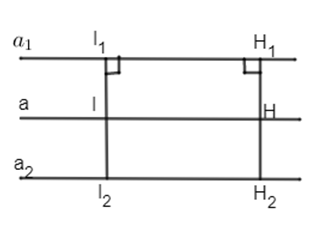
Gọi \({a_1},{a_2}\) là hai đường thẳng song song cho trước và h là khoảng cách giữa hai đường thẳng đó. Giả sử I là điểm cách đều hai đường thẳng và \({H_1};{H_2}\) là khoảng cách từ I đến hai đường thẳng đó.
Advertisements (Quảng cáo)
Ta có \({I_1}{I_2} = h \Rightarrow {H_1} = \dfrac{h }{ 2}\) (không đổi). Vậy I nằm trên đường thẳng a cách đường thẳng \({a_1}\) một khoảng bằng \(\dfrac{h }{2}.\)
Bây giờ: Lấy một điểm H thuộc đường thẳng a, dựng \(H{H_1} \bot {a_1}\) . Ta có \({H_1}{H_1}H\) là hình chữ nhật nên \(H{H_1} = {H_1} = \dfrac{h }{ 2}.\) Do đó điểm H cách đều đường thẳng \({a_1}.\) Tương tự đối với đường thẳng \({a_2}.\)
Advertisements (Quảng cáo)
Vậy tập hợp các điểm cách đều hai đường thẳng song song cho trước là một đường thẳng song song với hai đường thẳng đã cho và cách đều hai đường thẳng đã cho.


![[THCS Nam Đà] Thi kì 2 Ngữ Văn lớp 8: Tình yêu thiên nhiên trong thơ Bác](https://dethikiemtra.com/wp-content/uploads/2016/04/van-8-t2-100x75.jpg)