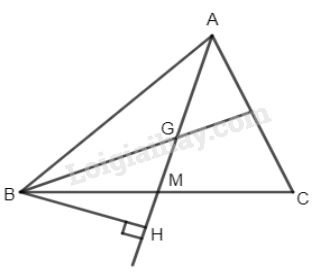
Gọi AM là trung tuyến và G là trọng tâm của \(\Delta ABC\) . Chứng minh: \({S_{BGM}} = \dfrac{1 }{ 6}{S_{ABC}}.\) … trong Đề kiểm tra 15 phút môn Toán học Chương 2 Hình học 8. Xem Đề và đáp án đầy đủ phía dưới đây

Gọi AM là trung tuyến và G là trọng tâm của \(\Delta ABC\) . Chứng minh: \({S_{BGM}} = \dfrac{1 }{ 6}{S_{ABC}}.\)

Vì AM là trung tuyến và G là trọng tâm của \(\Delta ABC\) ta có \(GM = \dfrac{1 }{3}AM.\)
Kẻ đường cao BH ta có: \({S_{ABM}} = \dfrac{1 }{ 2}AM.BH.\)
\({S_{BGM}} = \dfrac{1 }{ 2}GM.BH\)
Advertisements (Quảng cáo)
Mà \(GM = \dfrac{1}{3}AM\) (tính chất trọng tâm)
\( \Rightarrow {S_{BGM}} = \dfrac{1}{3}{S_{ABC}}\) mà \({S_{ABM}} = \dfrac{1 }{2}{S_{ABC}}\)
Advertisements (Quảng cáo)
Do đó: \({S_{BGM}} = \dfrac{1 }{6}{S_{ABC}}.\)