Luyện tập đường trung bình của tam giác, của hình thang: Đáp án và Giải bài 26, 27, 28 trang 80 SGK Toán 8 tập 1.
Bài 26. Tính x, y trên hình 45, trong đó AB // CD // EF // GH.
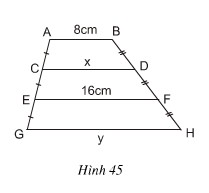
Gợi ý giải: Ta có AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường-trung bình của hình thang ABFE.
Do đó: CD = (AB +EF)/2 = (8+16)/2 = 12 cm
Hay x = 12 cm
Tương tự CDHG là hình thang, EF là đường-trung bình của hình thang CDHG.
Nên EF = (CD +GH)/2 ⇒ GH = 2EF -CD = 2.16 – 12
GH = 20 hay y = 20cm
Vậy x = 12cm, y = 20cm.
Bài 27 trang 80. Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF ≤ (AB+CD)/2
a) Trong ∆ACD có EA = ED, KA = KC (gt)
Advertisements (Quảng cáo)
nên EK là đường trungbình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trungbình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2= (AB +CD)/2
Vậy EF ≤ (AB +CD)/2
Advertisements (Quảng cáo)
Bài 28. Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thằng EF cắt BD ở I, cắt AC ở K.
a) Chứng minh rằng AK = KC, BI = ID.
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK
a) Vì EA = ED, FB = FC (gt)
Nên EF là đường-trung-bình của hình thang ABCD.
Do đó: EF // AB // CD
∆ABC có BF = FC và FK // AB
nên: AK = KC
∆ABD có AE = ED và EI // AB
nên: BI = ID
b) Vi EF là đường trung bình của hình thang ABCD.
nên EF = (AB+CD)/2 = (6+10)/2= 8
EI là đường-trung-bình của ∆ABD nên EI = ½.AB =½.6 = 3 (cm)
KF là đườngtrung-bình của ∆ABC nên KF =½.AB=½.6 = 3 (cm)
Lại có EF = EI + IK + KF
nên IK = EF – (EI + KF) = 8 – (3 + 3) = 2 (cm)
