Tóm tắt lý thuyết và Giải bài 20,21 trang 79; giải bài 22,23, 24,25 trang 80 SGK Toán 8 tập 1: Đường trung bình của tam giác, của hình thang – hình học.
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba,
Định lí 2: Đường-trung-bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
∆ABC, AD = DB, AE = EC => DE // BC, DE = 1/2BC
Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Định lí 1: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định lí 2: Đường-trung-bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
Đáp án và hướng dẫn giải bài tập trong SGK trang 79,80 SGK Toán 8 tập 1
Bài 20. Tìm x trên hình 41.

Giải: Ta có ∠K = ∠C = 500 nên IK // BC (∠K = ∠C(đồng vị))
Mà KA = KC suy ra IA = IB = 10cm
Vậy x = 10cm
Advertisements (Quảng cáo)
Bài 21. Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và OD = 3cm.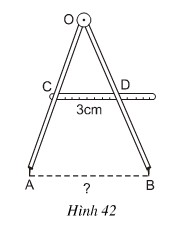
Giải: XétΔOAB Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD =1/2AB
Suy ra AB = 2CD = 2.3 = 6cm.
Bài 22 trang 80. Cho hình 43. Chứng minh rằng AI = IM.

Advertisements (Quảng cáo)
Xét ∆BDC có BE = ED và BM = MC (giả thiết) ⇒ ME là đường trung bình của ∆BDC
nên EM // DC Suy ra DI // EM
Xét ∆AEM có AD = DE và DI // EM nên AI = IM.
Bài 23. Tìm x trên hình 44.
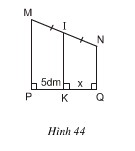
Giải: Xét tứ giác MNPQ có MP⊥PQ và NQ⊥PQ ⇒ MP//NQ ⇒ tứ giác MNPQ là hình thang
Mặt khác: IK⊥PQ và MP⊥PQ ⇒ IK//MP, MI=IN ⇒ IK là đường trung bình của hình thang MNPQ ⇒ KQ= KP = 5 dm ⇒x = 5 dm
Bài 24 trang 80. Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
Đáp án:
Kẻ AP⊥xy, BQ ⊥xy và CK⊥xy lần lượt tại P,Q,K
⇒ AP//CK//BQ ⇒ tứ giác APQB là hình thang
Mặt khác: AC = CB ⇒ CK là đường-trun- bình của hình thang APQB
⇒ CK = (AP+BQ)/2 = (12+20)/2 = 16 cm
Bài 25 trang 80 SGK Toán 8 hình học. Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.
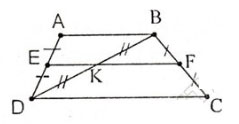
Ta có: EA = ED và KB = KD ⇒ EK là đường-trung bình của ΔDAB ⇒ EK//AB (1)
Ta có: FB = FC và KB = KD ⇒ FK là đường trung-bình của ΔBCD ⇒ FK//CD (2)
Mặt khác AB//CD (giả thiết) (3)
Từ (1),(2),(3) ⇒ EK//FK//AB
Qua K ta có EK và FK cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.



![[THCS Tân Viên] thi học kì 2 lớp 8 môn Địa: Hãy vẽ biểu đồ hình tròn thể hiện cơ cấu diện tích của ba nhóm đất chính của nước ta](https://dethikiemtra.com/wp-content/uploads/2020/09/anhbaitren13-100x75.jpg)


