Hướng dẫn giải bài 1,2,3,4,5 trang 115 SGK Toán 8 tập 1: Đa giác – Đa giác đều – chương 2 hình lớp 8
Bài 1. Hãy nêu cách nhận biết một lục giác lồi.
Học sinh tự vẽ phác một lục giác lồi. (Chẳng hạn lục giác lồi ABCDEF như hình bên)

Cách nhận biết một đagiác lồi: Một đa giác lồi là một đagiác thỏa mãn 2 điều kiện sau:
– Các cạnh chỉ cắt nhau tại các đỉnh, nghĩa là không có hai cạnh nào cắt nhau tại một điểm mà không phải là đỉnh. Một đagiác thỏa mãn điều kiện này là đagiác đơn.
– Đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa một cạnh tùy ý của nó. Một đa-giác đơn thỏa mãn thêm điều kiện này là đagiác lồi.
Bài 2. Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:
a) Có tất cả các cạnh bằng nhau;
Advertisements (Quảng cáo)
b) Có tất cả các góc bằng nhau.
HD: a) Hình thoi không có góc vuông, có tất cả các cạnh bằng nhau nhưng các góc không bằng nhau nên hình thoi không phải là đa-giác-đều.
b) Hình chữ nhật có tất cả các góc bằng nhau nhưng các cạnh không bằng nhau nên hình chữ nhật không phải là đa-giác-đều.
Bài 3 trang 115. Cho hình thoi ABCD có ∠A = 600 . Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.

Vì ABCD là hình thoi, ∠A =600 Nên ∠B= 1200 và ∠D = 1200
Advertisements (Quảng cáo)
+ Ta có: AB = AD và AE = EB, AH = HD ⇒ AE = AH ⇒ ΔAEH cân tại A.
Mà ∠A =600 nên ΔAEH đều ⇒ ∠HEB = ∠EHD = 1200 (Góc ngoài của Δ đều AEH) và HE = AE = HD.
+ Tương tự: ΔFCG đều ⇒ ∠BFG = ∠FGD = 1200 và FG = FC = BF.
Vậy lục giác EBFGDH có EB = BF = FG = DG = HD = HE.
Và ∠HEB = ∠B = ∠BFG = ∠FGD = ∠D = ∠DHE (cùng bằng 1200)
Suy ra EBFGDH là một lúc giác đều.
Bài 4 trang 115 toán 8 (hình) tập 1. Điền số thích hợp vào các ô trống trong bảng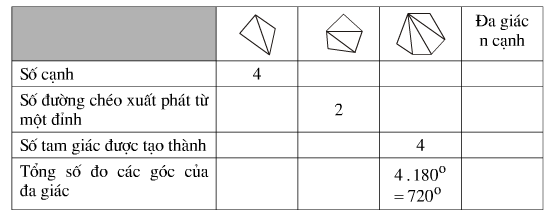
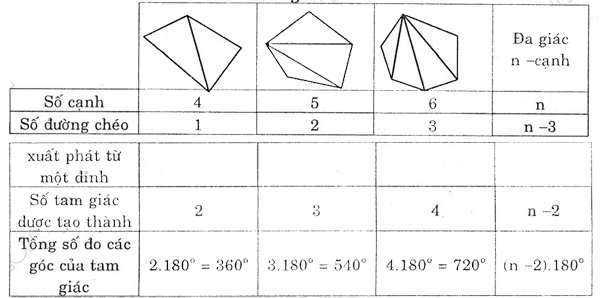
Bài 5. Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n- giác đều.
HD: Tổng số đo các góc của hình n- giác bằng (n – 2).1800 (bằng tổng số đo các góc của số tam giác được tạo thành bởi các cạnh và các đường chéo xuất phát từ 1 đỉnh). Vậy số đo mỗi góc của n – đa -giác-đều là:
![]()
Áp dụng công thức trên, ta có:
– Số đo mỗi góc của ngũ giác đều là
![]() = 1080
= 1080
– Số đo mỗi góc của lục giác đều là ![]() = 1200
= 1200






