Bài 1: Điểm thi môn tiếng Anh của một nhóm học sinh được ghi lại ở bảng sau:

Hãy cho biết:
a) Tần số của điểm 7.
b) Số các giá trị khác nhau của dấu hiệu.
c) Tính điểm trung bình của nhóm học sinh trên.
d) Tìm mốt của dấu hiệu.
Bài 2: Một nhóm học sinh làm bài kiểm tra môn Toán có điểm số như sau:

a) Dấu hiệu ở đây là gì? Có bao nhiêu học sinh làm bài?
b) Lập bảng “tần số” và nhận xét.
c) Tính số trung bình cộng và mốt của dấu hiệu.
Bài 3: Trung bình cộng của sáu số là 4. Do bớt đi một số thứ sáu nên trung bình cộng của năm số còn lại là 3. Tìm số thứ sáu.

Bài 1:
Advertisements (Quảng cáo)
a) Tần số của 7 là 4.
b) Số các giá trị khác nhau của dấu hiệu: 5.
c) Điểm trung bình:
\(\overline {\rm{X}} = \dfrac{{3 + 6.2 + 7.4 + 8 + 10}}{9}\)\( = \dfrac{{61}}{9} \approx 6,8.\)
d) Mốt của dấu hiệu: \({{\rm{M}}_0} = 7.\)
Bài 2:
a) Dấu hiệu là: “Điểm số của bài kiểm tra môn Toán của một nhóm học sinh”. Có 20 học sinh làm bài.
b) Lập bảng “tần số”:
Advertisements (Quảng cáo)

Nhận xét:
Số các giá trị của dấu hiệu: 20.
Số các giá trị khác nhau: 8.
Giá trị lớn nhất: 10.
Giá trị nhỏ nhất: 2.
Giá trị có tần số lớn nhất: 7.
Giá trị có tần số nhỏ nhất: 6; 10.
Giá trị chủ yếu thuộc khoảng từ 5 đến 7.
c) Điểm trung bình:
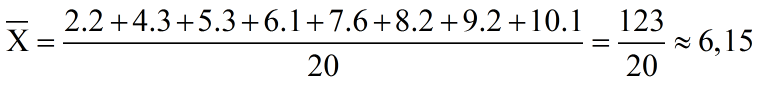
Mốt của dấu hiệu: \({{\rm{M}}_0} = 7.\)
Bài 3:
Gọi sáu số lần lượt là \(a,b,c,d,e,f.\) Theo bài ra ta có
\(\dfrac{{a + b + c + d + e + f}}{6} = 4\)
\( \Rightarrow {\rm{ }}\) \(a + b + c + d + e + f = 24\) (1).
Khi bớt đi số thứ sáu, theo giả thiết ta có
\(\dfrac{{a + b + c + d + e}}{5} = 3\)
\( \Rightarrow {\rm{ }}\) \(a + b + c + d + e = 15\) (2).
Từ (1) và (2) \( \Rightarrow {\rm{ }}\) \(f = 24 – 15 = 9.\)
Vậy số thứ sáu là 9.