Tia phân giác của góc: giải bài 30,31,32 ,33,34 ,35,36,37 trang 87 SGK Toán 6 tập 2.
Bài 30. Trên cùng một nửa mặt phẳng chứa bờ Ox, vẽ tia Ot sao cho ∠xOt =250 , ∠xOy= 500.
a) Tia Ot có nằm giữa hai tia Ox và Oy không?
b) So sánh ∠tOy và ∠xOt.
c ) Tia Ot có là tia phângiác của ∠xOy không? Vì sao?
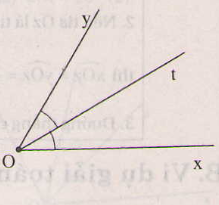
a) Tia Ot nằm giữa hai tia Ox và Oy (1) vì các tia Ot,Oy cùng thuộc nửa
mặt phẳng bờ chứa Ox và ∠xOt < ∠xOy
b) Tia Ot nằm giữa hai tia Ox,Oy nên:
∠xOt + ∠yOt = ∠xOy
do đó
250+ ∠tOy = 500
suy ra : ∠tOy = 500– 250 =250
Vậy : ∠xOt = ∠tOy (2)
Advertisements (Quảng cáo)
c) từ (1) và (2) suy ra Ot là tiaphângiác của ∠xOy.
Bài 31. a) Vẽ ∠xOy có số đo 1260
b) vẽ tia phângiác của ∠xOy ở câu a.
Bài 32 trang 87 . Khi nào ta kết luận được tia Ox là tia phângiác của ∠xOy? Trong những câu trả lời sau, em hãy chọn những câu đúng:
Advertisements (Quảng cáo)
Câu c) d) đúng.
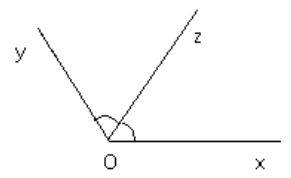
Bài 33 Toán 6 – hình học. Vẽ hai góc kề bù xOy, yOx’, biết ∠xOy = 1300.Gọi Ot là tiaphângiác của ∠xOy. Tính số đo ∠x’Ot.
Vì ∠xOy và ∠yOx’ là hai góc kề bù
nên ∠xOy + ∠yOx = ∠xOx’
hay 130º + ∠yOx’ = 180º
⇒ ∠yOx’ = 180º – 130º
⇒ ∠yOx’ = 50º
Vì Ot là tia-phân-giác của ∠xOy
nên ∠xOt = ∠tOy = ∠xOy/2 = 130º/2 = 65º
Vì tia Oy nằm giữa 2 tia Ot và Ox’
nên ∠tOy + yOx’ = tOx’
hay 65º + 50º = 115º
Vậy ∠tOx’ = 115º
Bài 34. Vẽ hai góc kề bù xOy và yOx’, biết ∠xOy = 1000 . Gọi Ot là tiaphân.giác của ∠xOy và Ot’ là tia-phân-giác của ∠x’Oy. Tính số đo các ∠x’Ot, xOt’, tOt’.
Do ∠xOy kề và bù với ∠x’Oy
∠xOy + ∠x’Oy = 180º
∠x’Oy = 180º – ∠xOy
∠x’Oy = 180º – 100º
∠x’Oy = 80º
Do Ot là tiaphângiác của ∠xOy nên:
∠xOt = ∠tOy = 100º/2 = 50º
Do Ot’ là phân giác của ∠x’Oy nên:
∠x’Ot’ = ∠t’Oy = 80º/2 = 40º
Tính ∠x’Ot = ∠x’Oy + ∠yOt = 80º + 50º = 130º
Tính ∠xOt’ = ∠xOy + ∠yOt’ = 100º + 40º = 140º
Tính ∠tOt’ = ∠t’Oy + ∠yOt = 40º + 50º = 90º
Bài 35 trang 87. Vẽ góc bẹt xOy. Vẽ tia.phângiác Om của góc đó. Vẽ tia phân giác Oa của∠xOm. Vẽ tia-phân-giác Ob của ∠mOy. Tính số đo ∠aOb.
Do Om là tia-phân-giác của góc bẹt
∠xOy = 180º
∠yOm = ∠xOm = 180º/2 = 90º
Do Ob và Oa lần lượt là tia.phân.giác của ∠yOm = xOm = 90º/2 = 45º = ∠bOm = ∠aOm
Tính ∠bOa
∠bOa = ∠bOm + ∠aOm = 45º + 45º = 90º
Bài 36 trang 87 Toán 6 hình tập 2
Cho hai tia Oy,Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết:
∠xOy = 30º ; ∠xOz = 80º
Vẽ tia.phân.giác Om của ∠xOy. Vẽ tia.phân.giác On của yOz. Tính ∠mOn.
 Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có:
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có:
∠ xOy = 30º < ∠xOz = 80º
nên tia Oy nằm giữa hai tia Ox và Oz.
Vậy ∠xOy + ∠yOz = ∠xOz
∠yOz = ∠xOz – ∠xOy = 80º – 30º = 50º
Vì tia Om là tia.phân.giác của ∠xOy nên
∠nOy = ∠zOy/2 = 25º
∠yOm = ∠xOy/2 = 15º
Vì Om là tia.phân.giác của ∠xOy nên
∠nOy = ∠zOy/2 = 25º
Vậy ∠nOm = ∠nOy + ∠yOm = 25º + 15º = 40º
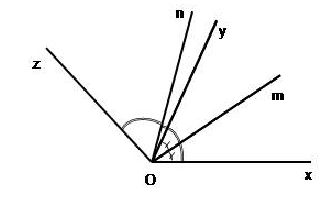
Bài 37 trang 87. Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết rằng
∠xOy =30º,∠xOz =120º
a) Tính số đo ∠yOz.
b) Vẽ tia phângiác Om của ∠xOy,tia phângiác On của ∠ xOz. Tính số đo ∠mOn
a) Tia Oy nằm giữa hai tia Ox, Oz, từ đó tính được:
∠ yOz = 1200– 300= 900
b) Tia Om nằm giữa hai tia Ox,On, từ đó tính được:
∠ mOn = 600– 150= 450







![[THCS Phạm Tuấn] thi học kì 2 môn Lý lớp 8 năm 2020: Tại sao xoong nồi thường làm bằng kim loại còn ấm, chén, bát đĩa lại thường làm bằng sứ?](https://dethikiemtra.com/wp-content/uploads/2020/07/82208322_457565911818124_3698770116704468992_n-100x75.jpg)




