Đáp án và hướng dẫn giải bài tập 79, 80, 81, 82 trang 108; bài 83, 84, 85, 86 trang 109 – Luyện tập SGK Toán 8 tập 1: Hình vuông – Chương 1 Tứ giác.
Bài 79. a) Một hình.vuông có cạnh bằng 3cm. Đường chéo của hình.vuông đó bằng 6cm, √18cm, 5cm hay 4cm ?
b) Đường chéo của một hìnhvuông bằng 2dm. Cạnh cảu hìnhvuông đó bằng: 1dm, 3/2dm, √2dm hay 4/3dm ?
Giải: a) Gọi đường chéo của hình vuông có độ dài là a.
Ta có: a2 = 32 + 32 = 18
Suy ra a = √18 (cm)
Vậy đường chéo của hình-vuông đó bằng 3√2 (cm).
b) Gọi cạnh của hình-vuông là a.
Ta có a2 + a2 + 22 ⇒2 a2 = 4 ⇒ a2 = 2 ⇒ a = √2 (dm)
Vậy cạnh của hình-vuông đó bằng √2(cm).
Bài 80. Hãy chỉ rõ tâm đối xứng của hìnhvuông, các trục đối xứng của hìnhvuông.
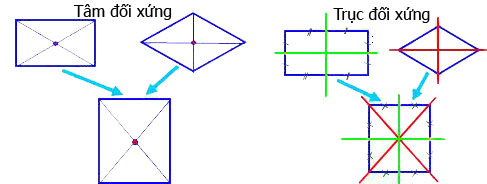Hình-vuông có 1 tâm đối xứng là giao điểm 2 đường chéo và 4 trục đối xứng là 2 đường chéo và 2 đường thẳng đi qua trung điểm các cạch đối của hình-vuông.
Bài 81 trang 108. Cho hình 106. Tứ giác AEDF là hình gì ? Vì sao ?
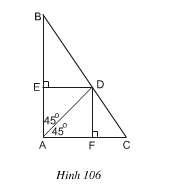
Tứgiác AEDF là hình vuông.
Giải thích:
Cách 1:
Tứgiác AEDF có EA // DF (cùng vuông góc AF)
DE // FA (cùng vuông góc với AE)
Suy ra AEDF là hình bình hành (theo định nghĩa)
Hình bình hành AEDF có đường chéo AD là phân giác của góc A nên là hình thoi.
Hình thoi AEDF có ∠A= 450+ 450= 900
Nên tứ giác AEDF là hình vuông.
Cách 2:
Advertisements (Quảng cáo)
Xét tứ giác EDFA có ∠A = ∠E = ∠F = 900 ⇒ EDFA là hình chữ nhật
mặt khác ∠EAD = ∠FAD = 450 ⇒ AD là phân giác góc ∠EAF
Suy ra AEDF là hình vuông.
Bài 82.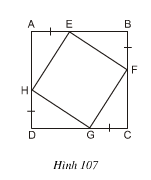
Cho hình 107, trong đó ABCD là hình-vuông. Chứng minh rằng tứ giác EFGH là hình-vuông.
Ta có :
AD = AB (ABCD là hình-vuông)
Hay AH + HD = BE + EA
Mà : HD = EA (gt)
⇒ AH = EB
Xét ΔAHE VÀ ΔBEF, ta có :
∠EAH = ∠FBE = 900(ABCD là hình vuông)
EA = BF (gt)
AH = EB (cmt)
⇒ ΔAHE = ΔBEF
⇒ HE = EF (1) và ∠AEH = ∠BFE
Mà : ∠BEF + ∠BFE = 900
Advertisements (Quảng cáo)
⇒ ∠AEH + ∠BFE = 900
⇒∠HEF = 900
chứng minh tương tự ta được : ∠GHE= 900 và ∠EFG = 900
⇒ Tứgiác ADEF là hình chữ nhật (2)
Từ (1) và (2), suy ra : ADEF là hình vuông.
Luyện tập bài 83,84,85,86 trang 109 Toán lớp 8 tập 1 phần hình học
Bài 83. Các câu sau đúng hay sai ?
a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.
b) Tứ-giác có hai đường chéo vuông góc nhau tại trung điểm của mỗi đường là hình thoi.
c) Hình thoi là tứ-giác có tất cả các cạnh bằng nhau.
d) Hình chữ nhật có hai đường chéo bằng nhau là hìnhvuông.
e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hìnhvuông.
Các câu sai: a)(Thiếu tại trung điểm mỗi đường) và d)
Các câu đúng: b), c), e).
Bài 84 trang 109. Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.
a) Tứ-giác AEDF là hình gi ? Vì sao ?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ-giác AEDF là hình thoi ?
c) Nếu tam giác ABC vuông tại A thì tứgiác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ-giác AEDF là hìnhvuông ?
Đáp án: Các em tự ghi giả thiết kết luận.
a) Ta có: DE // AF, DF // AE (gt)
⇒Tứ-giác AEDF là hình bình hành. (theo định nghĩa)
b) ) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc ∠BAC ⇒ D là giao điểm của phân giác góc ∠BAC với cạnh BC.
c) Khi ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông). ⇒ BD ⊥ AC tại tại trung điểm I mỗi đường.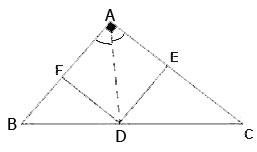
Hình chữ nhật ADEF là hìnhvuông ⇒ AD là phân giác của góc A ⇒ ΔABC vuông tại A và D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hìnhvuông.
Bài 85 trang 109 toán 8 tập 1. Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứgiác ADFE là hình gì ? Vì sao ?
b) Tứgiác EMFN là hình gì ? Vì sao ?
a) Xét ADFE ta có: AE // DF (Do AB//DC)
AE = EB, DF = FC
⇒ AE = DF nên tứgiác ADFE là hình bình hành. (1)
Ta có AD = AE và ∠EAD = 900 (2)
Từ (1) và (2) tứ-giác ADFE là hìnhvuông.
b) Ta có BE //DF và EB = BF ⇒ tứ.giác EBFD là hình bình hành ⇒ DE//FB (3)
Tương tự: AE//FC và AE = FC ⇒ tứ.giác AECF là hình bình hành ⇒ AF//EC (4)
Từ (3) và (4) ⇒ tứ.giác EMFN là hình bình hành
Mặt khác: tứ.giác ADFE là hình-vuông (cmt) ⇒ ME = MF và ME ⊥ MF ⇒ ∠ EMF = 900
⇒ tứ.giác EMFN là hình-vuông.
Bài 86 trang 109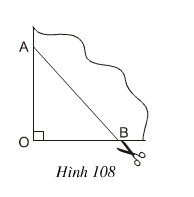 
Đố. Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứgiác. Tứ giác nhận được là hình gì ? Vì sao ? Nếu ta có OA = OB thì tứgiác nhận được là hình gì ?
Giải: Khi cắt một tờ giấy gấp làm tư theo nhát cắt AB. Khi mở tờ giấy ra,ta được 1 tứ-giác có 4 cạnh bằng nhau và hai đường chéo vuông góc với nhau tại trung điểm mỗi đường nên tứgiác đó là hình thoi.
Nếu OA = OB thì hình thoi có hai đường chéo bằng nhau nên tứ -giác đó là hình vuông.
![[THCS Phúc Chu] thi cuối học kì 2 lớp 8 môn Địa: Vẽ biểu đồ thích hợp thể hiện cơ cấu diện tích của ba nhóm đất chính của nước ta](https://dethikiemtra.com/wp-content/uploads/2020/06/canh-dong-100x75.jpg)
